Cog Conundrum

[Nigel Graham 2Participant @nigelgraham2]

… and before some Smart Alec complains, yes, the alliteration is deliberate!

.

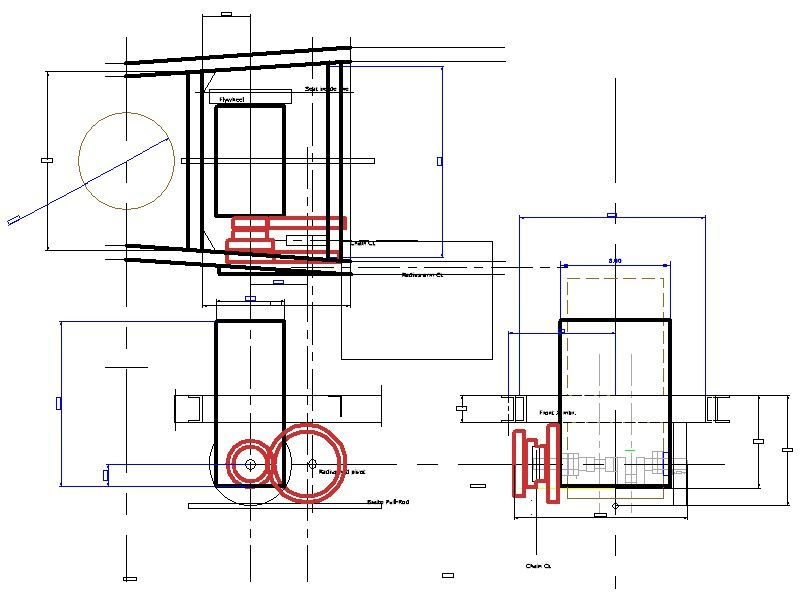
Designing my steam-wagon's two-speed, two-shaft gearing, I found that a long-saved pinion and gear set could give a reasonable low gear, allied to the sprocket reduction of the final drive, and will fit the chassis fairly well.

The wheels carry no identity marks, but careful measuring revealed metric dimensions, and 2 MOD size. So we need make the high gear also 2 MOD.

The existing wheels' tooth counts are 32 and 72, so the high-gear tooth-count sum needs also be 104.

So far so good.

'

Before buying the other wheels, equally obviously I need again verify the tooth counts, by physically counting using a felt-tip pen to "tick" them off and highlight the tens.

Also, I thought, test it by running the pinion, with one gullet marked, round its mate with one tooth marked.

'

That's where the fun starts.

The pinion's start gullet should meet main wheel tooth 64, remainder 8 left to go. Only it doesn't!

No end of repeats brought no solution; but revealed they reunite on the pinion's Circuit Number 4; again at 8, again at 12.

'

So I synthesised the problem by a simple spreadsheet consisting of a column of 1-32 repeats, alongside a column of 1-72 repeats.

That showed the pinion's start gullet should collect the main wheel start tooth on every 9th complete orbit of pinion round wheel. There, the accumulated main wheel tooth is the 288th by spreadsheet row number, an integer multiple of both 32 and 72. (By 9 and 4 respectively)

Only that does not happen when physically running the pinion round the wheel, on the table: it happens every 4 orbits.

I wondered if in fact the two wheels, of uncertain origin but apparently unused, are perhaps of MOD and DP formats, but they would run out of pitch only a short way round.

Or is the wheel of 71 teeth, my first count? That would not give this strange every-4 orbits behaviour, and the spreadsheet's 71s columns reveal the hunting action.

Count physically yet again: 72 teeth.

Then put the wheels away and go for a pint!

.

This matters because I am trying to verify what I need buy for the accompanying two gears for equal centres, yet these anomalies suggest my arithmetic is totally wrong.

So where am I going wrong, please?

.

[Yes I know I'd gain extra Brownie Points by cutting the wretched things myself but I want to finish the damn' vehicle before Nature finishes me, and I want the gears to work. The whole project has taken a ridiculously excessive time as it is! Besides, many professional engineering companies use stock gears, and probably did 100+ years ago, so if it's good enough for them….)

.

Oh, and there are such things as "cogs". Millwright-speak for the inserted teeth in mill gears, not the complete wheels. In flour mills they are of hardwood, running against cast, all-iron, pinions; a combination that crucially cannot spark, but as a by-product is also very smooth and quiet.

[Nigel Graham 2Participant @nigelgraham2]

[HopperParticipant @hopper]

Sounds right to me. If you have a 72 and a 32 tooth gear, after two revolutions of the 32T it should be engaging with the 64th tooth on the 72T, with 8 teeth left over. After repeating the pattern 4 times, you have accumulated the extra 4 x 8 teeth = 32 so the two marks line up again.

When you rotate the small gear two full revolutions, what tooth does its mark match up with on the big gear? It should be the 64. What are you getting?

Two gears that are meshing tooth-for-tooth can;t get out of pitch. A tooth is a tooth. If each tooth engages with the next gullet on the other gear, then there can be no "slippage" with a gear, unless one gear is riding up tip-to-tip over the other gear, which would be very readily apparent as the centre distance varied.. .

[JasonBModerator @jasonb]

"Only that does not happen when physically running the pinion round the wheel, on the table: it happens every 4 orbits".

 

When running the small wheel around the large one you need to allow for the fact the pinion is also making a rotation as it moves in a circle.

When both gears have fixed shafts that does not happen

 

Popular brain teaser is to ask how many times a pinion/circle/coin revolves around a larger one. Example

 

Edited By JasonB on 26/01/2023 07:43:43

[Brian GParticipant @briang]

Posted by JasonB on 26/01/2023 07:11:17:

"…

When running the small wheel around the large one you need to allow for the fact the pinion is also making a rotation as it moves in a circle…

I knew the opposite happened with sun and planet gears but had never considered this – always something new to learn here.

Brian G

[HopperParticipant @hopper]

Now, how counterintuitive is that? If you took the big circle and laid it out flat in a straight line the count would be different from when it is formed into a circle. Shows how much we can rely on "common sense".

And the steam lorry mystery is solved. Rotate both gears in situ and all will be well.

Now if you want to bend your mind a little further, check out this planetary gearing simulator link and set the sun gear to 36 teeth and two planetary gears to 18 teeth and observe that the marks line up every second revolution of the smaller gear  now.

Edited By Hopper on 26/01/2023 11:07:49

[John HinkleyParticipant @johnhinkley26699]

Nigel,

I'm not entirely sure what you are asking, but if I understand correctly, I have come up with the idea below:

Having nothing better to do while waiting for the new sofa and armchair to be delivered, I set about designing a Hi-Lo speed gear cluster, based on your dimensions in the OP. The Lo ratio gears are 32 and 72 tooth Mod 2 gears, 68mm and 148mm diameter respectively. For the Hi ratio pair, I selected 44 and 60 tooth Mod 2, to retain the same 104mm shaft spacing. This gives gear ratios of (Lo) 2.25:1 and (Hi), 1.36:1. The cluster shafts are 104mm apart. No allowance has been made for running clearances

The gears are selected by a simple fork arrangement running in a groove on the 32-44 tooth gear cluster.

To my my mind, those are big gears. I imagine your lorry will be a pretty substantial size when finished.

Make of it what you will, or ignore at your pleasure. Kept me occupied for an hour or so, anyway.

John

[Nigel Graham 2Participant @nigelgraham2]

My Goodness!

I had had no idea this would touch on some strange geometrical puzzles, when I simply thought the problem was my weak arithmetical skills!

Hopper –

I've just tried it again. I start with two marked root on the pinion straddling the tooth marked 1 on the wheel.

Two turns of the pinion takes the marks to straddle tooth 65!

..

Jason –

Assuming that puzzle to be a bit more subtle than just the ratio of the radii or diameter (3) I thought it would be how many times the small circumference divides into the larger.

So [6 pi / 2 pi]….

Err, = 3.

.

John,

Thank you for that analysis! What you have there is pretty much as I'd designed although with the two driving pinions face-to-face and between the two driven gears. That is to fit the space available and to cope with the chain sprocket being between the two larger gears. The chain dictates the layout of the gears, with the driving pinions on the end of the crankshaft. My thought is to use a selector-fork bridging the larger pinion, acting on its faces.

The ratios you give are as I'd calculated in the optimistic hope of the engine managing 400rpm as the prototype did. My sums give road speeds of about 2-1/2 mph using the two gears "in stock" and slightly under 4 mph. In theory…

The gears are quite big, yes, but not unduly so as the model's scale is 1/3 and some of the original catalogue photos do give glimpses of large, spoked gears under the nearside footplate.

I could though use 1.5 Mod gears (or inch equivalents) if I replace the two earmarked gears entirely.

Though one-third scale the model is not ever so large because its original was E.S. Hindley & Sons' "Light Delivery Van" , with capacities from 1 to 2 tons. (Their 5 and 7 ton "Standard" wagons were rather bare-looking undertypes with the engine geared directly to the axle – with the gear-lever apparently just in front of the rear off-side wheel.)

So it comes out at about 5 feet long by a shade under 2 wide on the rear axle: I slimmed it by a couple of inches so it would fit through the front door of my first home. The superstructure is a full 2ft wide as appeared correct to scale, and is relatively easy to remove as it does not support any working parts. The rear wheels are 12.75 diameter: their tyres are slices of steel pipe close to scale; though the front wheels, also of pipe slices, are a little under scale.

The canopy, based on a few photos, seems to have been an optional extra! Lorry drivers were 'ard in them days.

I took this photo of it at the MSRVS Rally in 2009….. it's not changed outwardly very much since! Though I have made a lot of parts.

[Nigel Graham 2Participant @nigelgraham2]

Not sure if this will work, or how legible it will be, but this is from the TurboCAD drawing in question…

The thick black outlines are the engine case and main chassis members. The thick red, the gears cited above.

The triangle apparent in plan but omitted from the elevations, is a part-made / provisional outer mounting-plate for the gear shafts. The chain-sprocket is between the two secondary gears, depicted by the rectangle of its basic envelope.

The faint brown outline is of the boiler, or parts of it.

Scale guide: the engine case, with the cylinders omitted here, is 8" wide by 5" front to back.

'

(The gears are shown by their pitch-circles: I cannot draw their teeth! Using just the PC plus the addendum and dedendum circles, is an old drawing convention anyway. It's in orthographic because I cannot draw anything even half as complicated as this, in 3D)

[Author]

Posts