diameter calculation

[Nicholas FarrParticipant @nicholasfarr14254]

Posted by Howard Lewis on 11/10/2019 16:14:05:

Being simple, I drew a circle with three chords 65 mm long. Then a 30/60/90 degree triangle, with one side being half the chord = 32.5 and used Sine or Cosine to calculate the Hypotenuse. Then doubled the answer to get the diameter, which my calculator said was 75.055535, if you want be frightfully accurate. Me? I'd settle for 75 as being about as good as i could get, although I might set the machine to 75.06 mm or 2.955 inches in old money.

That is about as complicated as my puny brain can tolerate.

Howard

Hi Howard, actually you don't need to half to cord, as you can use 65 divided by Sine 60 or Cosine 30 to give you the diameter directly. My original drawing shows using half a cord to get the radius directly, which is what someone asked for a while ago and of course Sine 60 would have given to same result.

Regards Nick.

[Michael GilliganParticipant @michaelgilligan61133]

Posted by 34046 on 12/10/2019 08:59:39:

.

Sorry Michael, but to my simple mind drawing it out with a ruler and a protractor is simple to me as opposed to elegant. May we just agree to disagree.

.

My turn to be sorry, Bill … I assumed that you would have constructed the equilateral triangle.

MichaelG.

[Neil WyattModerator @neilwyatt]

Posted by Andrew Johnston on 11/10/2019 14:17:32:

However, an algorithm to reach the answer quickly doesn't exist.

Andrew

Actually there are LOTS of algorithms that produce answers by paying off accuracy against speed.

As proven by Google Maps every day

[SillyOldDufferModerator @sillyoldduffer]

Posted by Michael Gilligan on 11/10/2019 22:32:03:

I’m relieved to see that we are in agreement, Andrew

My earlier point about accuracy comes down [in practical terms] to:

For Polar jobs, polar co-ordinates are ‘definitive’

For Rectangular jobs, rectangular co-ordinates are ‘definitive’

A classic example being the NEMA hole pattern for stepper motor flanges … devised as holes on a pitch-circle, but often specified as holes at each corner of a square [which requires expedient approximation].

MichaelG.

Oh dear, I'm going to disagree with Michael and Andrew. I believe cartesian and polar coordinates are completely interchangeable. This could end in tears!

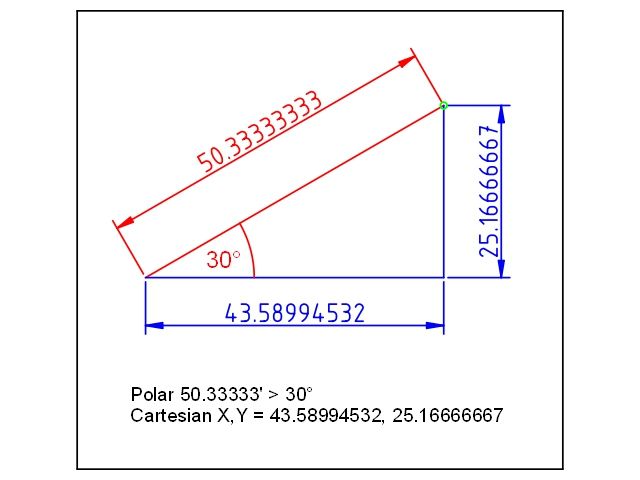
Consider this example where the centre of the green circle is defined in both polar and cartesian terms. The Polar definition in Red, Cartesian in Blue.

Now, although 30 degrees happens to be an integer, the distance to the green circle isn't. It's 50.3333 units recurring, which as drawn by QCAD can only be expressed to 8 places of decimals. At the same accuracy, the triangle defines the X coordinate as 43.58994532 and Y as 25.16666667 There's no particular reason why the distance in a polar coordinate need be a round number. Both cartesian and polar dimensions have the same limitation.

Consider also how 30 degrees in defined. As a convenience we think of it as a segment of a circle divided into 12 equal parts. In practice, dividing a circle isn't an accurate operation, in fact the best way to do it is to calculate the tangent to as many places of decimals as needed, and then to lay out the angle over a large baseline. Dividing Y by X is the tangent of the angle, and tangents can be calculated to as many places of decimals as reqiired.

I suggest the accuracy of both coordinate systems is decided by the limitations of the calculator, human or machine, not by the nature of coordinate systems themselves. The limits can be large or small – when calculations were done manually, Four Figure Tables would limit the accuracy of tan(30) to 0.5774. Now the bog standard MS-Windows calculator makes 0.57735026918962576450914878050196‬ available, and – if needed – far more accuracy can be delivered by an arbitary precision package like mpmath.

Given enough number crunching Polar and Cartesian coordinates can be interchangably expressed as the other. Which one gets is used is surely a matter of convenience. Navigating a ship using Cartesian coordinates is unnatural, whilst laying out a job on a milling table with polar coordinates is clumsy.

If the number system happens to to fall nicely on round numbers for a particular position one might look better than the other, but given enough positions don't both systems fail to be spot on with equal frequency?

Dave

[duncan webster 1Participant @duncanwebster1]

For more methods of working this out than you could possibly want see **LINK**

but if you've got access to a decent CAD system you can do it a lot faster and to an accuracy better than you can manufacture in a fraction of the time

Edited By duncan webster on 12/10/2019 21:43:15

[Michael GilliganParticipant @michaelgilligan61133]

Posted by SillyOldDuffer on 12/10/2019 21:17:48:

Oh dear, I'm going to disagree with Michael and Andrew. I believe cartesian and polar coordinates are completely interchangeable. This could end in tears!

[…]
Given enough number crunching Polar and Cartesian coordinates can be interchangably expressed as the other.
[…]

 

.

No, Dave … that simply cannot be true

… Herewith, my tears

Pi is a transcendental number and [with specific exceptions] there is no way that: “Given enough number crunching Polar and Cartesian coordinates can be interchangably expressed as the other.”

Specific exceptions would, for example, include four equi-spaced points on a pitch circle which are located at 12, 3, 6, and 9 o’clock positions: because those points can be ‘properly expressed’ in either system.

MichaelG.

.

P.S. … Your statement that “Dividing Y by X is the tangent of the angle, and tangents can be calculated to as many places of decimals as reqiired.” also gives the lie to your claim. Because if the systems were truly interchangeable, then every tangent value would be finite.

Edited By Michael Gilligan on 12/10/2019 22:30:54

[Alan Waddington 2Participant @alanwaddington2]

To quote my old gaffers well used phrase

“Come on lads, we’re not making gold watches here”………..

[Jeff DaymanParticipant @jeffdayman43397]

Agree Alan, it's getting ridiculous again, isn't it? Mind you, the egg cup I made this week was accurate to 22 millionths of an inch, and well worth the effort……

My goodness what a waste of time. The OP just wanted to know a shop grade calculation (and got one early on) .

[Kiwi BlokeParticipant @kiwibloke62605]

'My goodness what a waste of time. The OP just wanted to know a shop grade calculation (and got one early on) .'

So the thread served its original purpose, and quickly. Now it's moved on to an intellectual discussion about other, but still related things. What's wrong with that? Whose time is being wasted? If a few old codgers wish to spend time in a virtual pub, close to a virtual fireplace, bouncing ideas around, should anyone complain? If this forum confined itself to answering questions, it would be a dull place indeed. I have posted to ask questions, to inform, to challenge, to entertain and to get people to think. I don't intend to stop. Naturally, not all of my posts will have been appreciated by all watchers. That probably goes for all other posters too. Too bad. I hope the thought police aren't welcome here.

[Kiwi BlokeParticipant @kiwibloke62605]

SOD. ' In practice, dividing a circle isn't an accurate operation, in fact the best way to do it is to calculate the tangent to as many places of decimals as needed, and then to lay out the angle over a large baseline. Dividing Y by X is the tangent of the angle, and tangents can be calculated to as many places of decimals as reqiired.'

I don't agree that tan calculation is a good way to divide, because as X tends to zero, the calculation becomes difficult to handle in practice, as the tan tends towards infinity.

I think the key is 'in practice', especially when engineering, rather than theoretical maths is concerned. In practice, we would use whatever hardware we have at our disposal to do the job. Polar to Cartesian translation makes sense if our machines can only cope with rectilinear movements, but when a rotary table is available, or something like a BCA or Boley UFR milling machine can be used, it would probably be sensible to use polar co-ordinates, if that's how the job has been specified. The accuracy we can achieve in practice is far less than the calculation accuracy achievable by cheap scientific calculators, so in practice, translating between co-ordinate systems isn't going to damage accuracy. Theory is another matter…

[not done it yetParticipant @notdoneityet]

Slide rules were good enough to design and calculate all the dims for the SR71 spy plane back in the last century before computers, along with others requiring less precision.

They would not provide too many significant figures – but enough for a plane to travel at over mach 3. Some slide rules were likely a lot larger than our pocket versions, but they were not computer designed, either!

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Jeff Dayman on 13/10/2019 00:34:16:

Agree Alan, it's getting ridiculous again, isn't it? Mind you, the egg cup I made this week was accurate to 22 millionths of an inch, and well worth the effort……

My goodness what a waste of time. The OP just wanted to know a shop grade calculation (and got one early on) .

.

Jeff,

The question was answered, to the OP’s satisfaction, long ago.

The discussion has evolved.

Fact of Life … That’s how it goes.

Please give the whinging a rest.

MichaelG.

[Michael GilliganParticipant @michaelgilligan61133]

Posted by SillyOldDuffer on 12/10/2019 21:17:48:
.

Oh dear […]

.

Dave,

In deference to Mr Dayman’s sensitivities [*], I have sent you a personal message.

MichaelG.
.

[*] Sarcasm reared its ugly head in his post; so he’s obviously upset !

Edited By Michael Gilligan on 13/10/2019 08:50:41

[Nicholas FarrParticipant @nicholasfarr14254]

Hi, yes, the question was answered to the OP's satisfaction, If one finds that the evolved thread becomes of no more interest to them, then they are not forced to read it any further, but of course it still interests others.

Regards Nick.

[HopperParticipant @hopper]

And we haven't even started to calculate how many angels can dance on the head of a pin of the diameter with three chords this size. I know the plain diameter formula has been posted on here before somewhere, but not encompassing the chords aspect.

[Gary WoodingParticipant @garywooding25363]

Just to dot all the 'I's, here is my 'proof' of Nick's solution.

It depends on two properties of chords in circles, and the Sine rule of trigonometry.

1. All angles subtended on one side by a chord to any point on the circumference are equal, so in the diagram, angle C equals angle D.

2. If the chord is a diameter, the angle is 90°, and conversely, if the angle subtended by a chord is 90° then the chord is a diameter.

3. The Sine rule states that, for any triangle, Sin A/a = Sin B/b = Sin C/c

In the diagram, A, B, and C, are the three random points, and the circle is their PCD. You want to calculate the length of its diameter.

Choose any side of the triangle ABC (side AB in the diagram) and draw a perpendicular line from one end to to meet the circle. This is the dashed line BD.

Because they both come from chord AB, angles C and D are equal, so SinC = SinD.

But SinD = c/h, so h = c/SinD = c/SinC

But angle ABD is a right angle, so h = the diameter of the circle.

[Nicholas FarrParticipant @nicholasfarr14254]

Hi Gary, a better way of proving the Sine rule works for the example 26 diagram is shown below. This is a half size one but the relationship between the angle and the length of the two sides shown are the same. This shows the integrity of the 41 degree angle and the lengths of the original sides and should help show those who don't quite understand how it works. The extended line B-A becomes the diameter of the PCD for A, B and C and a new PCD drawn on the centre of this line will show the Right Angle Triangle with the red line at a right angle to line B and C and it will be noticed that the new PCD will pick up both ends of the red line and point B.

Excuse the makeshift real world drawing, all the dimensions are close to those actually calculated.

Regards Nick.

Edited By Nicholas Farr on 13/10/2019 18:18:25

[Anonymous]

Posted by Neil Wyatt on 12/10/2019 19:10:29:

Actually there are LOTS of algorithms that produce answers by paying off accuracy against speed.

I doubt they use algorithms in the sense of reaching a definitive answer without a full search, although probably in the sense that the sequence is gauranteed to halt. I suspect the answers are more likely based on heuristics.

If Google has an algorithm that solves the travelling salesman problem then I expect they're in line for the Fields Medal.

Andrew

[Howard LewisParticipant @howardlewis46836]

There's no hope for me!

I could never work to better than two places with a 10" Faber Log-Log Slide rule. And now am WELL out of practice. (Still have it somewhere! )

Hopper did not specify the units of the diameter, or the tolerance thereof, of the head of the pin on which we have to have our angels dancing!

Howard

[Neil WyattModerator @neilwyatt]

Posted by Andrew Johnston on 13/10/2019 18:43:24:

Posted by Neil Wyatt on 12/10/2019 19:10:29:

Actually there are LOTS of algorithms that produce answers by paying off accuracy against speed.

I doubt they use algorithms in the sense of reaching a definitive answer without a full search, although probably in the sense that the sequence is gauranteed to halt. I suspect the answers are more likely based on heuristics.

If Google has an algorithm that solves the travelling salesman problem then I expect they're in line for the Fields Medal.

Andrew

Solving it accurately isn't the issue, it's just the time taken. There are algorithms that speed things up, for example by calculating a near-optimal solution then testing alternatives based on it.

The record for an accurate solution appears to be about 89,500 locations.

en.wikipedia.org/wiki/Travelling_salesman_problem

But there are LOTS of practical algorithms that trade absolute accuracy for huge increases in speed.

[Neil WyattModerator @neilwyatt]

Posted by Nicholas Farr on 13/10/2019 18:14:19:

Hi Gary, a better way of proving the Sine rule works for the example 26 diagram is shown below. This is a half size one but the relationship between the angle and the length of the two sides shown are the same. This shows the integrity of the 41 degree angle and the lengths of the original sides and should help show those who don't quite understand how it works. The extended line B-A becomes the diameter of the PCD for A, B and C and a new PCD drawn on the centre of this line will show the Right Angle Triangle with the red line at a right angle to line B and C and it will be noticed that the new PCD will pick up both ends of the red line and point B.

Excuse the makeshift real world drawing, all the dimensions are close to those actually calculated.

Regards Nick.

Edited By Nicholas Farr on 13/10/2019 18:18:25

That's excellent & elegant.

[Nicholas FarrParticipant @nicholasfarr14254]

Hi Neil, thanks for your comment. The drawing is a bit rough and ready, but the 41 degree angle and the three points were set quite accurately and I think it shows what might seem to be an obscure triangle.

Regards Nick.

[duncan webster 1Participant @duncanwebster1]

Posted by Gary Wooding on 13/10/2019 10:38:21:

Just to dot all the 'I's, here is my 'proof' of Nick's solution.

It depends on two properties of chords in circles, and the Sine rule of trigonometry.

1. All angles subtended on one side by a chord to any point on the circumference are equal, so in the diagram, angle C equals angle D.

2. If the chord is a diameter, the angle is 90°, and conversely, if the angle subtended by a chord is 90° then the chord is a diameter.

3. The Sine rule states that, for any triangle, Sin A/a = Sin B/b = Sin C/c

In the diagram, A, B, and C, are the three random points, and the circle is their PCD. You want to calculate the length of its diameter.

Choose any side of the triangle ABC (side AB in the diagram) and draw a perpendicular line from one end to to meet the circle. This is the dashed line BD.

Because they both come from chord AB, angles C and D are equal, so SinC = SinD.

But SinD = c/h, so h = c/SinD = c/SinC

But angle ABD is a right angle, so h = the diameter of the circle.

That's really elegant, but just to be pedantic, don't you need to use the cosine rule to find angle C to start the whole thing off rather than sin rule

[SillyOldDufferModerator @sillyoldduffer]

Posted by Howard Lewis on 13/10/2019 21:35:36:

There's no hope for me!

I could never work to better than two places with a 10" Faber Log-Log Slide rule. And now am WELL out of practice. (Still have it somewhere! )

Hopper did not specify the units of the diameter, or the tolerance thereof, of the head of the pin on which we have to have our angels dancing!

Howard

Oh dear, I seem to have stirred up a hornets nest by putting my foot in it again! For the record, my comments about extreme accuracy of calculation relate to the properties of Polar and Cartesian coordinates, not to Paul's original question.

By asking about a practical problem, Paul opened the door to some interesting mathematical solutions and related problems. I questioned the assertion that Polar Coordinates are intrinsically more accurate than Cartesian Coordinates by suggesting both systems are equivalent provided the calculations are done to a sufficiently large number of decimal places. (Not convinced this is correct and Michael has set me some homework!) I wasn't suggesting Paul or anyone else needs to do hard sums in their workshops!

The maths might seem obscure and irrelevant, but it's vital to engineering. For example, a variation of Andrew's 'Travelling Salesman Problem' has a workshop application. It's used to find the most economic way of cutting shapes from sheet material, important when stuff is stamped from metal, and very common issue in off-the-shelf tailoring. Micro-economies aren't worth the effort in a home workshop, but pennies matter hugely when millions are made.

If maths is considered off-topic I apologise, but I've found value in all the posts, and don't mind at all that the conversation has opened out.

Ta,

Dave

[Michael GilliganParticipant @michaelgilligan61133]

Posted by SillyOldDuffer on 14/10/2019 10:09:03:

[…]

For the record, my comments about extreme accuracy of calculation relate to the properties of Polar and Cartesian coordinates, not to Paul's original question.

By asking about a practical problem, Paul opened the door to some interesting mathematical solutions and related problems. I questioned the assertion that Polar Coordinates are intrinsically more accurate than Cartesian Coordinates by suggesting both systems are equivalent provided the calculations are done to a sufficiently large number of decimal places. (Not convinced this is correct and Michael has set me some homework!) I wasn't suggesting Paul or anyone else needs to do hard sums in their workshops!

[…]

.

.

For the avoidance of doubt, Dave

What I intended to assert was not that “Polar Coordinates are intrinsically more accurate than Cartesian Coordinates”

But that ”for situations where Polar Coordinates properly specify the geometry, their use is intrinsically more accurate than a conversion to Cartesian Coordinates”

… It’s a subtle difference, but important.

MichaelG.

[Author]

Posts