Strength of Beams

[John MCParticipant @johnmc39344]

For a book that would help with the calculation side of this topic I would heartily recommend "Strength of Materials" by Geoffrey H Ryder. I've had a copy most of my working life. Still using it now.

I've also used Roark's and Shipley's books on the subject.

John

[Sam Longley 1Participant @samlongley1]

Posted by Martin Kyte on 10/09/2020 11:39:03:

Re castellated beam

Interesting way they make those. The webs are cnc cut (Water jet or Plasma) so that the two half profiles stack inside each other to fit onto a blank less than the final width of the finished web. The 'points are then butt welded to form a web with a series of circular hole down the middle. Add top and Bottom and you have your castellated beam.

regards Martin

Just one point– They are not normally circular holes but hexagonal. That gives flat surfaces for the weld at the new meeting point.

Going back to the OP's post & comment about the ruler. It is certainly stronger on edge.

Just an itemt that may solve a problem for someone. If they want a beam for a construction in a house etc, then a piece of flat plate the depth of the joists (or slightly less), bolted betweem 2 timber joists makes an excellent beam. It is cheap, & can be inserted into construction easily. Plasterboard etc can be easily nailed to it without awkward noggins etc. Herringbone noggins can be added in the space as normal if required to avoid rotation

 

Edited By Sam Longley 1 on 11/09/2020 08:06:32

[DC31kParticipant @dc31k]

Posted by duncan webster on 11/09/2020 00:02:28:

These ladies were known as 'computers'

I thoroughly endorse your recommendation of Gordon's books.

Not only do they deal with traditional engineering materials of concrete and steel, but also give very good accounts of building in stone, as well as interesting discussion of nature's own building materials, wood, bone and sinew.

On the 'computers' issue, applied to the US space program, the book 'Hidden Figures' is very good.

[JAParticipant @ja]

Posted by John MC on 11/09/2020 07:25:30:

For a book that would help with the calculation side of this topic I would heartily recommend "Strength of Materials" by Geoffrey H Ryder. I've had a copy most of my working life. Still using it now.

I've also used Roark's and Shipley's books on the subject.

John

Ryder took me through college and then I sold it. It is one of the few text books I wish I had kept.

JA

[DC31kParticipant @dc31k]

Posted by Sam Longley 1 on 11/09/2020 07:54:51:

Just one point– They are not normally circular holes but hexagonal. That gives flat surfaces for the weld at the new meeting point.

It is horses for courses.

The traditional ones give long spans for efficient material use, good for single-storey warehouses and industrial buildings.

However, when it comes to multi-floor construction (office space), the circular ones are much more popular. They allow the myriad of building services to pass through the holes in the web rather than under the bottom flange. This means the overall structural depth can be reduced, allowing more than one extra floor (with its per square foot rent).

Where rectangular holes are needed, they can be incorporated, usually with stiffener ribs above and below the opening.

The march of technology has also had an influence. Traditional castellated beams were cut out of pre-existing rolled sections. Most modern cellular beams are cut from three plates and welded together. This gives you a lot more choice on both flange thicknesses and widths and also web height. CNC profiling and automatic welders facilitate this.

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Sam Longley 1 on 11/09/2020 07:54:51:

Just one point– They are not normally circular holes but hexagonal. That gives flat surfaces for the weld at the new meeting point.

.

I suppose that would depend upon one’s definitions of ‘they’ and ‘normally’

As I mentioned yesterday:

_____

Here’s an interesting page:

**LINK**

Edited By Michael Gilligan on 10/09/2020 21:34:21

_____

MichaelG.

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Sam Longley 1 on 11/09/2020 07:54:51:

Going back to the OP's post & comment about the ruler. It is certainly stronger on edge.

.

Sorry to be a bore, Sam … but :

whilst certainly stiffer, I think stronger remains interestingly debatable.

MichaelG.

[DC31kParticipant @dc31k]

I am glad that people are slowly coming to the conclusion that the question is unanswerable as posed.

For a given area of material, anything other than a regular shape (circle, equilateral triangle, square, etc.) can be made to have an almost infinite second moment of area.

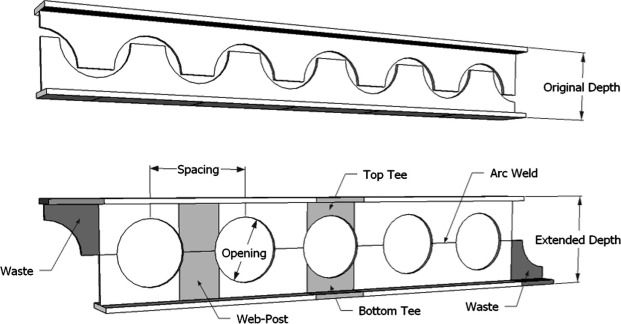
Take the I-beam, for example. I read that gold can be hammered to 4 millionths of an inch thick. So use 1% of the material to make a web of this thickness and divide the rest of the material between the two flanges.

Totally impractical as a real-world object but fits the question very well.

A little thought on the first example given in the original post would show the form of the question presents difficulties.

You do not need to be Superman to deflect a rectangle on edge. Take a ruler and try it. Press not too hard and it will buckle out of the plane of the applied load. And that is the problem every real-world engineer has to face. Pushing on things in one way induces forces and effects in another.

A more simple example is compression. Intuitively, why would we expect a structure to behave much differently when we squash it as opposed to when we pull it apart? But it does. And this has been known since Euler's time.

So when we bend something, we have both tension and compression (and anyone who has ever cut a branch of a tree will know this) and the member subject to bending will inherit some of its behaviour from both of these.

[Nicholas FarrParticipant @nicholasfarr14254]

Posted by Sam Longley 1 on 11/09/2020 07:54:51:

Posted by Martin Kyte on 10/09/2020 11:39:03:

Re castellated beam

Interesting way they make those. The webs are cnc cut (Water jet or Plasma) so that the two half profiles stack inside each other to fit onto a blank less than the final width of the finished web. The 'points are then butt welded to form a web with a series of circular hole down the middle. Add top and Bottom and you have your castellated beam.

regards Martin

Just one point– They are not normally circular holes but hexagonal. That gives flat surfaces for the weld at the new meeting point.

Going back to the OP's post & comment about the ruler. It is certainly stronger on edge.

Just an itemt that may solve a problem for someone. If they want a beam for a construction in a house etc, then a piece of flat plate the depth of the joists (or slightly less), bolted betweem 2 timber joists makes an excellent beam. It is cheap, & can be inserted into construction easily. Plasterboard etc can be easily nailed to it without awkward noggins etc. Herringbone noggins can be added in the space as normal if required to avoid rotation

 

Edited By Sam Longley 1 on 11/09/2020 08:06:32

Hi Sam, well not always hexagon, in fact most lorry trailers that I've seen with castellated beams had what you might call a clipped diamond shape. But whatever shape they are, it's the term that is used for this type of beam.

Of course back before water jet, plasma cutting and CNC were around, they were flame cut and in many cases by skilled people.

Regards Nick.

Edited By Nicholas Farr on 11/09/2020 11:01:49

[ZanParticipant @zan]

The “strength” of the beam we are talking about is bending I.e stiffness

If I remember back correctly to my engineering classes, any beam in bending, the strength is simply width * depth ^3. (Cubed) so double the with and double the stiffness,  but double the depth It goes up from 1to 8 As the beam is in both tension and compression then there is zero force at its centre(neutral axis) resulting that  most of the material in the beam should be placed as far from the neutral axis as possible, hence the economy of the I beam in both terms of material used and it’s weight .

The problem is in resisting flexing ((sideways deflection and twisting). The ruler being very thin for its depth will Easily flex sideways . Applying this to the boring bar is interesting as the resultant forces are neither vertical or horizontal so directly but as the cutting point extends outside its geometric form then there is an additional rotational component The bar is cantilevered at the tool post, but the bit is cantilevered at right angles to that.  Very complex! So round or square would be best  and as big as possible!

in his articles about boring bars, G Thomas talked about the bar with the bit clamped by a push rod along its axis and commented on how little difference the hole for the rod made to the stiffness of the bar

Edited By Zan on 11/09/2020 11:49:31

Edited By Zan on 11/09/2020 11:56:34

[Nicholas FarrParticipant @nicholasfarr14254]

Posted by Zan on 11/09/2020 11:45:39:

The “strength” of the beam we are talking about is bending I.e stiffness

The problem is in resisting flexing ((sideways deflection and twisting).

Edited By Zan on 11/09/2020 11:49:31

Edited By Zan on 11/09/2020 11:56:34

Hi putting this with SOD's hanging a load on the end is fine, but lifting the same load that is not sideways perpendicular with the beam maybe a different matter altogether and the further away from sideways perpendicular the load is, the worse the situation becomes and can lead to permanent distortion or even failure of the beam.

Regards Nick.

[Sam Longley 1Participant @samlongley1]

Posted by Michael Gilligan on 11/09/2020 08:25:52:

Posted by Sam Longley 1 on 11/09/2020 07:54:51:

Just one point– They are not normally circular holes but hexagonal. That gives flat surfaces for the weld at the new meeting point.

.

I suppose that would depend upon one’s definitions of ‘they’ and ‘normally’

As I mentioned yesterday:

_____

Here’s an interesting page:

**LINK**

Edited By Michael Gilligan on 10/09/2020 21:34:21

_____

MichaelG.

The example you refer to with circular holes is not what I was referring to. If one wants to put a cut along the web of a beam then separate the 2 halves & offset & then re weld to form a deeper castellated beam one needs an edge to weld to. If the line was a wavey one the meeting points would not meet in a way which could be suitably welded & the holes would NOT be circular. Standard castellated beams cut from a simple I beam would be cut such that the line has flat edges for the weld. The hexagonal hole thus remaining would still leave room for services & I do not recall having difficulty installing them. I did fit quite a few tonnes of the stuff in a number of new schools halls etc But I do confess, that was 40 years ago & things move on, so If I am wrong then I stand corrected

The example in the one in the link would , presumably, be cut from an I beam with considerable waste.

[John MCParticipant @johnmc39344]

Posted by JA on 11/09/2020 08:16:52:

Posted by John MC on 11/09/2020 07:25:30:

For a book that would help with the calculation side of this topic I would heartily recommend "Strength of Materials" by Geoffrey H Ryder. I've had a copy most of my working life. Still using it now.

I've also used Roark's and Shipley's books on the subject.

John

Ryder took me through college and then I sold it. It is one of the few text books I wish I had kept.

JA

Have a look at the secondhand copies for sale on Amazon, postage costs more than the book.

I worked with Geoff Ryder, the author, for a few years. With out a doubt an extremely intelligent man who could right a very good book, but ask him to explain something verbally, oh dear……

John

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Sam Longley 1 on 11/09/2020 13:00:24:

.

The example you refer to with circular holes is not what I was referring to.

.

Sorry, Sam … My misunderstanding

I did try to cover that possibility with my opening line:

[quote] I suppose that would depend upon one’s definitions of ‘they’ and ‘normally’ [/quote]

MichaelG.

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Sam Longley 1 on 11/09/2020 13:00:24:

.

The example in the one in the link would , presumably, be cut from an I beam with considerable waste.

.

Here’s a direct quote from the linked page:

The top and bottom tees are frequently cut from different rolled sections, with the resulting asymmetric Westok beam formed with each tee/flange designed to suit the load it resists and the restraint conditions which apply locally.

.

From which it seems clear that there are many ways to skin these cats

MichaelG.

[Howard LewisParticipant @howardlewis46836]

As Zan says, stiffness is B x D^3 / 12, which is fairly easy to calculate for a square or rectangular beam.

But a circular, hexagonal, octagonal, or any irregular section surely will require an integration based on depth and width starting at Zero and increasing to the maximum depth, based on a formula taking into account the actual section, circular or otherwise.

Don't ask me to derive the formulae!

Howard

[HopperParticipant @hopper]

Posted by Sam Longley 1 on 11/09/2020 13:00:24:

Posted by Michael Gilligan on 11/09/2020 08:25:52:

Posted by Sam Longley 1 on 11/09/2020 07:54:51:

Just one point– They are not normally circular holes but hexagonal. That gives flat surfaces for the weld at the new meeting point.

.

I suppose that would depend upon one’s definitions of ‘they’ and ‘normally’

As I mentioned yesterday:

_____

Here’s an interesting page:

**LINK**

Edited By Michael Gilligan on 10/09/2020 21:34:21

_____

MichaelG.

The example you refer to with circular holes is not what I was referring to. If one wants to put a cut along the web of a beam then separate the 2 halves & offset & then re weld to form a deeper castellated beam one needs an edge to weld to. If the line was a wavey one the meeting points would not meet in a way which could be suitably welded & the holes would NOT be circular. Standard castellated beams cut from a simple I beam would be cut such that the line has flat edges for the weld. The hexagonal hole thus remaining would still leave room for services & I do not recall having difficulty installing them. I did fit quite a few tonnes of the stuff in a number of new schools halls etc But I do confess, that was 40 years ago & things move on, so If I am wrong then I stand corrected

The example in the one in the link would , presumably, be cut from an I beam with considerable waste.

Less waste than you might think when you look at the cunning way they are made with modern CNC cutting gear.

[Martin KyteParticipant @martinkyte99762]

. . . and as I said less weld too.

regards Martin

[SillyOldDufferModerator @sillyoldduffer]

Here's how Fusion 360 predicted three 60mm long Aluminium beams of equal cross-sectional area and length would deflect with a 250N load on the end.

Winner is tube, 13mm od, 11.34mm id, deflects 0.06mm

2nd square section 10x10mm, deflects 0.17mm

3rd round bar, 11.28mm diameter, deflects 0.22mm

Deflection is magnified above reality in the image to emphasie it. The colours indicate degree of deflection, not safety. Red highlights points of maximum deflection, not that the structure is going to break. Another FEM reports shows the structure has a 7x safety factor.

Although tube is stronger weight for weight than box or rod, the fact doesn't help us design a better boring bar because the diameter of the tube is bigger, and boring bars have to fit into small holes! Other structures make good use of tubes.

Dave

Edited By SillyOldDuffer on 12/09/2020 21:27:54

[Alan Waddington 2Participant @alanwaddington2]

Posted by Hopper on 12/09/2020 12:23:43:

Posted by Sam Longley 1 on 11/09/2020 13:00:24:

Posted by Michael Gilligan on 11/09/2020 08:25:52:

Posted by Sam Longley 1 on 11/09/2020 07:54:51:

Just one point– They are not normally circular holes but hexagonal. That gives flat surfaces for the weld at the new meeting point.

.

I suppose that would depend upon one’s definitions of ‘they’ and ‘normally’

As I mentioned yesterday:

_____

Here’s an interesting page:

**LINK**

Edited By Michael Gilligan on 10/09/2020 21:34:21

_____

MichaelG.

The example you refer to with circular holes is not what I was referring to. If one wants to put a cut along the web of a beam then separate the 2 halves & offset & then re weld to form a deeper castellated beam one needs an edge to weld to. If the line was a wavey one the meeting points would not meet in a way which could be suitably welded & the holes would NOT be circular. Standard castellated beams cut from a simple I beam would be cut such that the line has flat edges for the weld. The hexagonal hole thus remaining would still leave room for services & I do not recall having difficulty installing them. I did fit quite a few tonnes of the stuff in a number of new schools halls etc But I do confess, that was 40 years ago & things move on, so If I am wrong then I stand corrected

The example in the one in the link would , presumably, be cut from an I beam with considerable waste.

Less waste than you might think when you look at the cunning way they are made with modern CNC cutting gear.

I think castellated beams traditionally had hexagonal holes, because they were hand burned using an oxy acetylene torch. Straight lines are easier to burn by hand than circles. They bend like bananas when cut, we used to tack them together in a jig using metal wedges to straighten the halves back up.

[Roger BestParticipant @rogerbest89007]

Nice to see some engineering discussion.

How about suggesting what frequency the tool will resonate at and what surface finish will result?

[Robert Atkinson 2Participant @robertatkinson2]

I'm a bit late to this but a couple of points

on "Computers" I highly recommend the Film "Hidden Figures" Even SWMBO liked it.

Boring bars also require torsional stiffness. I beams have poor torsional stiffness.

Elliptical and teardrop tubes are used on aircraft in place or round for aerodynamic reasons not structural

When I worked for a acttual aircraft manufacturer (Norman Aeroplane Company, sheet metal in one end of the factory, aircraft out the other) in the mid 80's they still calculated stress, strain and strength manually (with calculators). No finite element analysis like Nastran. The critical structures like wings were then tested to ultimate (failure). The boss, Desmond Norman, would be very unhappy if the caluulaed and actual ultimate loads were out by more than a few percent.

Robert G8RPI.

[Author]

Posts