Michael,
OK, so your equation is this (slightly rewitten).

The first thing is that the numbers, 0.75 / 5 / 5, don't really add anything. The 0.75 just scales the height of the fence to that value, and the 5's scale the values of x and y. A very common thing to do in maths in this sort of situation is to "normalise" the equation by removing scale factors if they can be restored easily if you want them but otherwise just clutter up the working. In this case we would just re-write the equation like this.

So first I've scrubbed out the 0.75 as we can just multiply whatever value we get from the equation later by simple multiplication. Second I've removed the 5s (or actually the 25s as the 5s are squared) – if you wanted the result for particular values in the original formula you'd just multiply those values by 25 and insert the result in the second formula. It already looks simpler. Next it's written as "e to the minus()" as 1/anything is anything to the power -1. That isn't essential but looks tidier.
You probably know that e is the so-called Euler's constant, or the base of natural logarithms. It's a bit like pi, turns up all over the place in maths. It equals 2.7182818284590452353602874713527….and goes on for ever.
e to the power of something, or exp(something), gets very large very quickly as the something increases, it's exponential. So exp(1) = 2.717…; exp(2) = 7.389; exp(5) = 148.4…; exp(10) = 22,000.5; exp(25) = 72,004,899,337.4! As we have the reciprocal of the exponential in our formula, it gets very small very quickly. But also note that exp(0) = 1.
So if x and / or y in our formula above were zero, the function is equal to one. x and / or y are zero along the top edges of the fence, so that's why the top is flat.
Now imagine an ant exploring the surface carrying a tiny GPS that tells him his coordinates including height. Suppose that the y axis points North and the x axis points east. (And the earth is flat!) Now the ant crawls eastwards along a line of latitude "1" from say x=-5 to x=5. Along that line, since y equals 1, we could write the equation:

At y=-5 the value of z is 1/72,004,899,337.4 = next to nothing! Since x is squared, z has the same value at x=+5. At x=+2 or -2, z is 0.018, so still pretty small. x=+/-1 gives z=0.37. You can see why we get the "fence" since the function gets very small very quickly.
If the ant crawled along y=2, the function would be

Since the value of the exponent is now 4 times larger, z is much smaller except when x is (if you like) 4 times closer to zero. This why the fence gets sharper as you get further from the origin.
Incidentally, the function in the third equation is, except from some normalising factors, the same as the statistical "normal distribution" or "gaussian function". So the original function is a sort of two-dimensional gaussian (but in the real 2-d gaussian x squared and y squared are added not multiplied).
I hope this explanation helps. Generally with most of the formulas you could apply similar technicques, by first getting rid of multiplying coefficients and then looking at the behaviour of the function if you keep one variable constant and vary the other, and do that for various "constant" values. In effect you will be producing cross-sections of the shape. The App should easily allow you to do that.
 Michael Gilligan.
Michael Gilligan.

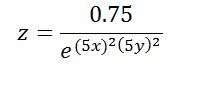
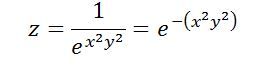
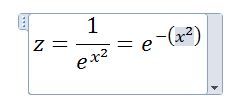
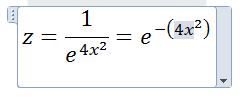

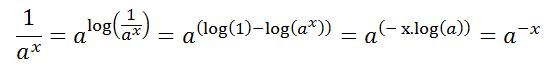

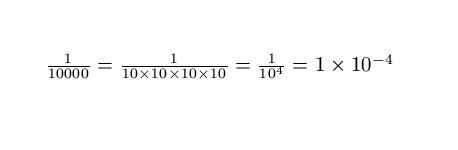
 I have known a few graduates that wanted to do maths initially but didn't 'cause they thought it was probably too hard. What I found very difficult was that ok it may be wonderful that things are like that but what on earth do you use the maths for.
I have known a few graduates that wanted to do maths initially but didn't 'cause they thought it was probably too hard. What I found very difficult was that ok it may be wonderful that things are like that but what on earth do you use the maths for.

