a little diversion

[MacolmParticipant @macolm]

People are not taking this seriously! To consolidate the confusion, what if the small circle rolls inside the large one?

Edited By Macolm on 11/10/2021 14:07:49

[Tony Pratt 1Participant @tonypratt1]

Macolm, I think people [me] are confused enough as it is.

Tony

[Rod RenshawParticipant @rodrenshaw28584]

Wonderful puzzle.

I think I have convinced myself the answer is 4. Malcolm's diagram is very clear.

The original question asked was "How many times does the circle "A" revolve in total?

and NOT "How many times does the circle "A" rotate about circle "B"?

So, A rotates around its own centre 3 times, and A also rotates once around the centre of B. So, 3+1 =4.

I think the same argument also applies to the situation where A is inside B.

This is one of those situations where one has to concentrate on answering the question as asked. Can't see many at Westminster being able to cope with this.

Rod

[Tony Pratt 1Participant @tonypratt1]

Final answer is 3, confused no more, I reckon the videos have been spoofed the maths doesn't lie.

Just seen Rod's answer, it then becomes a question of interpretation which is a whole different argument & poor question setting.

Tony

Edited By Tony Pratt 1 on 11/10/2021 14:49:04

[Tim StevensParticipant @timstevens64731]

It does seem, as Ron Renshaw suggests, that an O level in any science subject disqualifies anyone seeking election to Parliament. What a state the wonderful traditional public schools and universities have got us into! Sorry, into which they have got us.

Tim

[duncan webster 1Participant @duncanwebster1]

Sorry Tony, you're confused, it's definitely 4, and to answer Malcolm's question, 2.

[Anthony KnightsParticipant @anthonyknights16741]

I'm sorry gentlemen, but it seems obvious to me that the difference between the centres of the the

two circles is 3r + r = 4r. What's the problem?

[Martin ConnellyParticipant @martinconnelly55370]

Yes, 4. If you look at Malcom's diagram the small wheel rotates 120° around from the top to the point where the small wheel's A is next to the large wheel's A the small wheel has rotated 1 + 1/3 turns. When it has gone around another 120° to the point where the two A marks are together the small wheel has now done 2 +2/3 turns. By the time it gets back to the top it has done 3 + 3/3 = 4 turns.

Martin C

[Rod RenshawParticipant @rodrenshaw28584]

This problem gets better or is it worse?

After scrolling down David's link following David's suggestion to Michael, I am beginning to think my earlier answer of 4 might be wrong.

Is there a difference between "Revolve" and "Rotate"? While it true that Circle A rotates 3 times in it's circuit around Circle B, are any of these "turns" actually revolutions? The poster posits that a revolution means going around something else, a fixed point, and by implication turning on one's own axis is not a revolution. I know we often use these words almost interchangeably, but we can be more precise.

The question asks "How may times does Circle A revolve?" Since the only fixed point we have in this line drawing is Circle B, and Circle A only goes around Circle B once, should the answer be !?

Any other answers?

Rod

[Anonymous]

You've been reading the original thread, haven't you Rod?

[Nicholas FarrParticipant @nicholasfarr14254]

Hi Rod, according to my dictionary, both revolve and rotate can be; 1, "to orbit a central point" 2, "to turn on an axis" the term revolution can mean; 1, "orbital motion about a fixed point" 2, "a turning or rotational motion about an axis" so I guess they all mean much the same thing in this context. All three of these words have other definitions as well.

Regards Nick.

Edited By Nicholas Farr on 11/10/2021 19:00:27

[Gary WoodingParticipant @garywooding25363]

If both circles were the same size, would the right answer be 1 or 2? It's a question of definition, surely.

[Nicholas FarrParticipant @nicholasfarr14254]

Hi, I don't think anyone is suggesting that the maths are telling lies, and we all know that the circumference of circle B is three times that of circle A and the ratio therefore is three to one, which means there must be four revolutions to a cycle. Circle B is not rotating, but the whole configuration is still a ratio of three to one, and for circle A to complete one cycle, there has to be four revolutions and the only thing revolving is circle A.

Regards Nick.

[Nicholas FarrParticipant @nicholasfarr14254]

Hi Gary, I think it's a case of two for the price of one, as one cycle and one rotation would take place in the same time and space.

Regards Nick.

Edited By Nicholas Farr on 11/10/2021 19:27:16

[Rod RenshawParticipant @rodrenshaw28584]

Peter – I was reading the 32 nd poster responding to the original post on the Practical Machinist website, and to which I was signposted by David's suggestion to Michael. Are you saying there was a previous thread on this forum, if so I was not aware of it, I was just trying to keep this "diversion" moving.

Nick – thanks for the definitions. I was more or less quoting the 32 nd poster I referred to above, and who seemed quite precise and authoritative about his understanding that a revolution must be around a fixed point.

As someone has said there may be several answers depending on one's interpretation of the problem and the question. I can't imagine the original question setter could have imagined how much entertainment his/ her question would generate.

Rod

[Martin KyteParticipant @martinkyte99762]

3 rotations and a translation or orbit. Translations are not rotations.

regards Martin

[Anonymous]

Posted by Rod Renshaw on 11/10/2021 17:46:52:

Is there a difference between "Revolve" and "Rotate"? While it true that Circle A rotates 3 times in it's circuit around Circle B, are any of these "turns" actually revolutions? The poster posits that a revolution means going around something else, a fixed point, and by implication turning on one's own axis is not a revolution.

Seems demonstrably untrue. We commonly talk about revolutions per minute of a motor shaft.

[Anonymous]

Posted by Rod Renshaw on 11/10/2021 19:43:15:

Peter – I was reading the 32 nd poster responding to the original post on the Practical Machinist website, and to which I was signposted by David's suggestion to Michael.

Rod, yes that was the "original thread I was referring to" ….. and there should have been a winkie at the end of my post (a weak attempt at humour) – my apologies.

[Michael GilliganParticipant @michaelgilligan61133]

This comes with no explanation, but is worth a look : **LINK**

MichaelG.

.

Edit: __ Now watch this one: https://youtu.be/Xh5coE5wJ2I

 

Edited By Michael Gilligan on 12/10/2021 00:19:53

[Alan CharlestonParticipant @alancharleston78882]

Hi,

It's funny how a problem like this can get stuck in your head. I think I have finally sussed it out and for what it's worth this is what I have come up with.

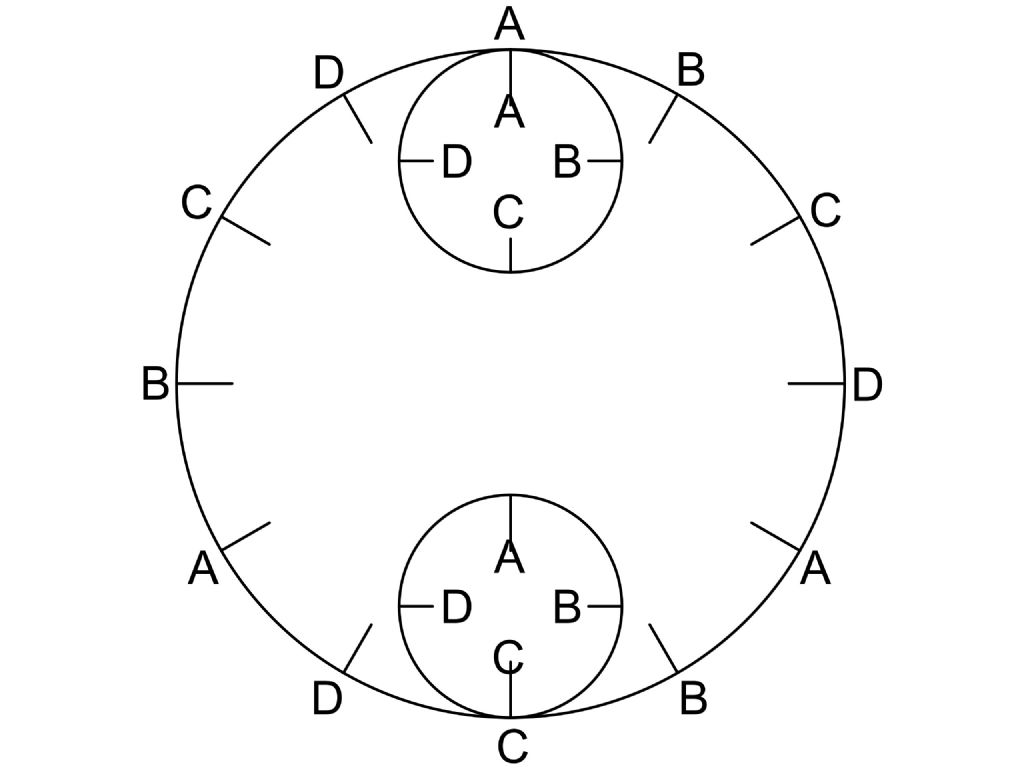
If we refer to Macolms drawing there are two forms of rotation going on here.

The first of these is the rotation of the small wheel around the axis of the large wheel. If the 2 circles have smooth circumferences and the small circle is rotated from the 12 o'clock position to the 3 o'clock position around the centre of the large circle without rotating about its own axis (rolling), the A point on the small circle will change from the 6 o'clock to the 9 o'clock position which gives an apparent clockwise rotation about the axis of the small circle of 90 degrees.

The second form of rotation is the small circle rotating about its own axis (rolling). If we assume the large circle to be a 120 tooth gear and the small circle to be a 40 tooth gear (3:1) then rolling the small gear from 12 to 3 o'clock will involve 120/4 = 30 teeth meshing which will cause the small gear to rotate by 30/40 X 360 = 270 degrees.

The total apparent rotation of the small circle is therefore 90 + 270 = 360 degrees which gives a total of 4 apparent rotations per full traverse of the large circle. This is made up of 3 rotations about the axis of the small wheel and 1 rotation about the axis of the large wheel.

Interestingly, this problem doesn’t arise when the large circle is rotated about the small circle. While playing with a 28 tooth gear and a 56 tooth gear, I could see that the small gear apparently rotated 3 times when circumnavigating the large gear instead of the intuitively expected twice.

When the large gear was rolled around the small gear however, things went as expected, with the large gear rotating 180 degrees for the first circuit and 360 degrees to complete the second.

I think this contradicts the “mathematical solution” presented in the video Michael linked to:

**LINK**

Regards,

Alan C.

[not done it yetParticipant @notdoneityet]

Do remember that this was a GCSE level question, not a degree level thesis discussion. Half (or more) GCSE students are poor at reading the questions properly, let alone answering the question actually asked.

[Michael GilliganParticipant @michaelgilligan61133]

Posted by not done it yet on 12/10/2021 08:30:54:

Do remember that this was a GCSE level question …

.

Do they have GCSE in the United States ?

… or are you saying it is an equivalent level ?

MichaelG.

.

https://www.princetonreview.com/college/sat-information

Edited By Michael Gilligan on 12/10/2021 08:51:58

[Nicholas FarrParticipant @nicholasfarr14254]

Hi Alan, the maths works just the same for your 28 & 56 gears, the ratio being two to one, 1+2=3, so three turns for the 56 round the 28 or visa-versa. It works just the same for gears that don't have a whole number for the ratio, e.g. a 100T & 30T gear has a ratio of 3.333> to 1, therefore it will take four and one third revs for the 30T to orbit the 100T gear once and 13 revs of the small gear to get it back to it's starting state.

Starting state.

First orbit @ 4 – 1 / 3 revs.

Second orbit @ 8 – 2 / 3 revs.

The third orbit takes it back to the starting state, i.e. 3 x 4.333> revs = 13 revs in total.

Regards Nick.

Edited By Nicholas Farr on 12/10/2021 10:01:19

[Michael GilliganParticipant @michaelgilligan61133]

Ref. __ **LINK**

https://www.nytimes.com/1982/05/25/us/error-found-in-sat-question.html

MichaelG.

[Author]

Posts