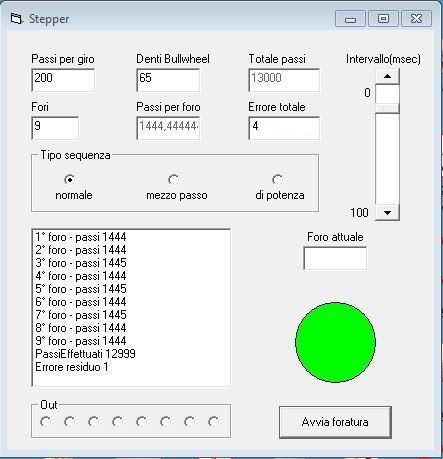
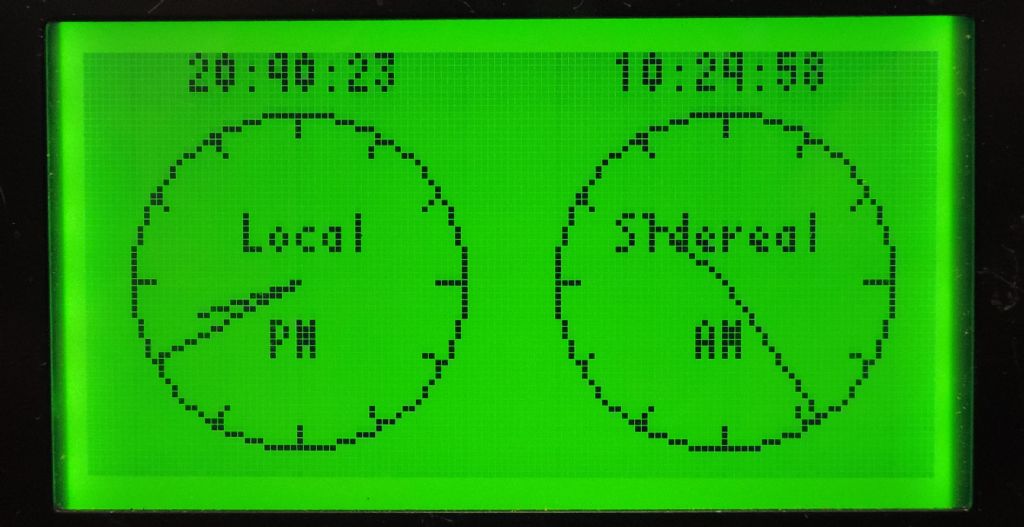
Electronic Indexers – How Is Cumulative Error Avoided?
Electronic Indexers – How Is Cumulative Error Avoided?
- This topic has 53 replies, 15 voices, and was last updated 5 July 2019 at 16:42 by
sam sokolik.
- Please log in to reply to this topic. Registering is free and easy using the links on the menu at the top of this page.
Latest Replies
Viewing 25 topics - 1 through 25 (of 25 total)
-
- Topic
- Voices
- Last Post
Viewing 25 topics - 1 through 25 (of 25 total)
Latest Issue
Newsletter Sign-up
Latest Replies
- UK Steel Supplier? 125 x 125 x 50 BMS
- Boiler Design – issue 4765
- Which Carbide Lathe Tools?
- Suggestions for next clock build?
- rotational motion into linear motion – force calculation?
- The strange phenomenon of Liquid Death
- Just How Many File Types Do We Need?
- quality 3 and 4 jaw chucks
- Obscure Thread
- Miniature parts maker in Leicester?