calculation for a sine bar

[brickyParticipant @bricky]

I am going to make an R8 gear cutting arbour and have been trying to work out the packing for a sine bar to set the taper turning attachment.The included angle for the taper is 16.51deg and I have calculated the vertical at 18.23 with trig,.I am not confident that I am correct,could some kind soul give verify this answer please.I havn't done trig since 1964 so remembering is a struggle.

Frank

[brickyParticipant @bricky]

[AdrianRParticipant @adrianr18614]

What is the centre distance (hypotenuse) on your sine bar?

Adrian

[old martParticipant @oldmart]

It depends how long the bar is. I have two 5" and one 2" at the museum, and I recently saw a 10" one on ebay. There are probably plenty of metric ones about as well.

Just put this calculator in your browser favourites:

 

http://www.carbidedepot.com/formulas-trigright.asp

Edited By old mart on 10/06/2020 19:33:35

[JasonBModerator @jasonb]

That would be right for a 5" bar

[brickyParticipant @bricky]

No wonder I can't get my head around trig,The sine bar is 5".

Frank

[JasonBModerator @jasonb]

I just use CAD, enter angle an 127 and it gives the height

[Martin ConnellyParticipant @martinconnelly55370]

The sine of the half angle (8.425 deg) is 0.1465. For a 5" sine bar the gauge block stack for this angle is 5*0.1465 = 0.7325"

Martin C

This is based on an angle of 8 deg 51 mins. I think some diagrams have this as 8.51 degrees. Not sure which is correct.

Edited By Martin Connelly on 10/06/2020 19:47:15

[AdrianRParticipant @adrianr18614]

Well the value 18.23 is right for 16.51 degrees but I don't think the angle is correct. I think it is 16 degrees 51 minutes which is 16.85 degrees. That would give 18.61 mm

Does anyone definitively know the angle as I have seen some other forums arguing what the angle is.

Adrian

[JasonBModerator @jasonb]

Model Engineers Handbook has it as 16deg 51 mins so that's 18.607mm

Edited By JasonB on 10/06/2020 19:50:01

[brickyParticipant @bricky]

Thanks for your confirming my effort ,I can proceed with confidence.

Frank

[Martin ConnellyParticipant @martinconnelly55370]

Crawford collets has 8 deg 25 mins for the half angle. Seems conclusive that people who are using 16.5 degrees have misread (or copied someone else who has misread) the angle when written as degrees and minutes as a decimal value.

Martin C

[AdrianRParticipant @adrianr18614]

I too am thinking of making an arbour, what is the best steel to use without hardening or grinding?

Adrian

[Martin ConnellyParticipant @martinconnelly55370]

I think for most home workshop machines the motor will stall before any steel arbour for an R8 spindle bends, as long as you don't make it really skinny.

Martin C

[old martParticipant @oldmart]

I have the lathe taper turning attachment set for MT2. It was set by length bars and trigonometry, but even that didn't get it exact. It ended up finally by trial and error using a MT socket as a gauge to feel the exact angle. Unfortunately, R8 sockets to test don't seem to exist, unless you have a mill spindle laying about. It is important to have your tool height exactly dead on or the taper will not be a cone.

I don't attempt to make an R8 arbor from scratch while soft ended blank ones are easy to get hold of.

https://www.ebay.co.uk/itm/RDGTOOLS-R8-SOFT-END-BLANK-END-ARBOUR-7-16-UNF-DRAWBAR-BRIDGEPORT/370487538089?hash=item5642c731a9:g:2~QAAOSwolVc-hCl

Edited By old mart on 10/06/2020 21:47:44

Edited By old mart on 10/06/2020 21:50:44

[not done it yetParticipant @notdoneityet]

I don't attempt to make an R8 arbor from scratch while soft ended blank ones are easy to get hold of.

Same here with MT2 (which are much cheaper and with more choice of end size). Shrink fit (and pin?) a shaft and machine to size. Job done.

[brickyParticipant @bricky]

I like a challenge and want to make steps on the arbour for saws as well as gear cutters.I think that a one piece unit will have more rigidity.

Frank

[SillyOldDufferModerator @sillyoldduffer]

Posted by AdrianR on 10/06/2020 19:42:21:

…

Does anyone definitively know the angle as I have seen some other forums arguing what the angle is.

 

Adrian

Not found a definitive 'R8' yet! It's not in my copy of Machinery's Handbook (20th Edn), which led me to assume R8 was just ANSI Standard Steep Machine Taper, 3½" to the foot, or 16.2602°. Not so!

Tubal Cain's Model Engineer's Handbook 3rd Edn and this link quoted as a Wikipedia reference both give 16 degrees and 51 minutes, which is 16.85° in decimal money. Tubal Cain and Wikipedia's Bridgeport collet drawings differ slightly, but the angle is the same. I think 16.85° is trustworthy.

R8 probably isn't in Machinery's Handbook because it's not a standard taper. (ie not recognised by ANSI, BS, DIN, ISO or other standards body.) Rather R8 started as a proprietary Bridgeport taper and since the patent expired has survived due to the wide popularity of the well-known Bridgeport milling machine. The rest of industry looks to have standardised on 3½" to the foot, but there are lots of different formats.

R8 doesn't seem to have any particular merit as as a home workshop taper. It's a quick release type not that different to the International Standard steep taper. Looking at the drawings R8 collets are lighter with a smaller gripping area, ie not so strong. I'd guess being smaller and lighter suits smaller mills better than the hefty standard collets found on machines bigger than a Bridgeport. Does R8 have any advantage over MT on a hobby sized mill other than quick release? I doubt it!

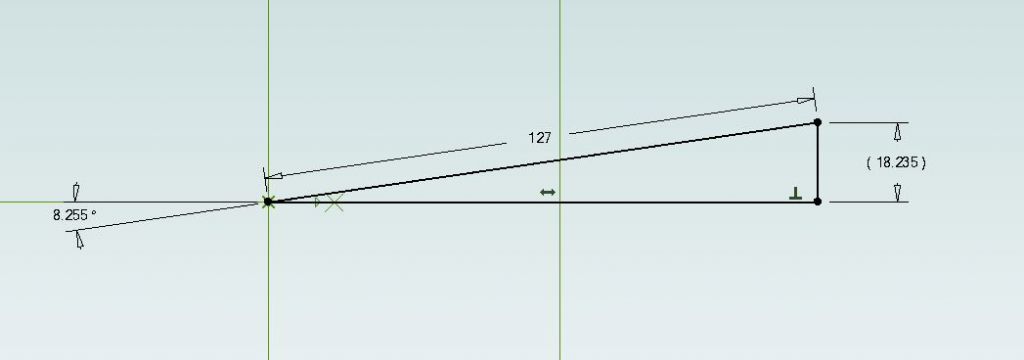
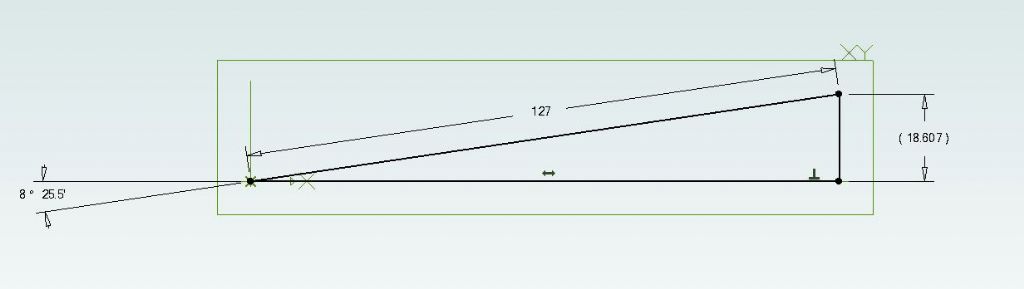
Confusion abounds, but my figures agree with Jason's. A 5" sine bar should be lifted by 18.607mm ( 0.7325" ) to set a taper half-angle of 8.475°

Have to say I found the maths quite error prone. Specifying angles in degrees, minutes and seconds is 'difficult' compared with decimal degrees. As most calculators work in radians, there's a few conversions to get wrong or forgetting to set the machine correctly. 16°51' = 16.85° = 0.2941 radians. After remembering to divide the angle by two, then recall from soh, cah, toa that the wanted height is 'o for opposite', hence height = sin(angle) X length of sine bar. Just to add to the fun, given a 5" sine bar, Jason worked in millimetres, same as me. I also used QCAD to check the result; I can't think of a quicker or safer way to get the answer. A human friendly drawing plus a computer doing the sums is hard to beat.

Why is nothing ever easy? Doesn't help I spent so many Maths Lessons staring out the window thinking about girls…

Dave

Edit: pesky smileys!

Edited By SillyOldDuffer on 11/06/2020 10:56:49

[Martin ConnellyParticipant @martinconnelly55370]

I had Sharp EL-531GH calculator to hand when I first looked at this. It lets me put in angles as degrees, minutes and seconds and to convert to decimal values and back.

Martin C

[Howard LewisParticipant @howardlewis46836]

If the included angle is 16.51 degrees, the half angle is 8.255 degrees. Sin 8.255 is 0.1435789.

To incline it at 8.255 degrees, a 5 inch Sine bar would need to be raised by 5 (0.1435789 ) inches which is 0.7178949 Inches or 18.234531 mm.

So 18.235 mm should be fairly close, but some slight lapping may still be needed for an exact fit..

Howard

[AdrianRParticipant @adrianr18614]

When I was at school I had Miss Clarkson as my teacher. A woman who struck fear in all the kids. Tweed clad, Short, rotund with a mop of grey hair Einstien would have been proud of. To finish the image off, she had a witches wart complete with hair on her nose.

I had trouble remembering the trig formula until I made up Some Old Hag (Sin = Opposite/Hypotenuse) Can Always Help (Cos = Adjacent/Hypotenuse) To Oil Aircraft (Tan = Opposite/Adjacent).

I now look back on her with fondness, she went out of her way to get me into A level maths after failing my O level. She even gave me lunchtime lessons three days a week.

Adrian

[Howard LewisParticipant @howardlewis46836]

We were taught that "Some People Have, Curly Brown Hair, 'Til Painted Black" as a similar aide memoire.

One of the few bits of school maths that I can still recall, (DON'T ask about calculus! )

Howard

[Andrew TinsleyParticipant @andrewtinsley63637]

Hello Old Mart,

George Thomas, debunked the oft quoted "Tool must be exactly on center height, if cutting a taper". He showed by calculation and practice that the tool could be significantly off center before it became apparent in the taper.

See his book Model Engineering Workshop Manual, Tee Publishing.

Andrew.

[JasonBModerator @jasonb]

Posted by SillyOldDuffer on 11/06/2020 10:55:05:

 

Not found a definitive 'R8' yet! It's not in my copy of Machinery's Handbook (20th Edn), which led me to assume R8 was just ANSI Standard Steep Machine Taper, 3½" to the foot, or 16.2602°. Not so!

It's in the one I have as 16deg 51' 

First item under "collets"

Edited By JasonB on 11/06/2020 13:13:40

[Chris Evans 6Participant @chrisevans6]

I seem to recall information for all the common collet/arbor tapers are in ARC's catalogue. I have several homemade R8 arbors all turned to this information and checked to "Blue" in the Bridgeport spindle. Easier to get right on an R8 than a morse because the R8 is so much shorter.

[Author]

Posts