Closing the chapter on meshing

[Sam StonesParticipant @samstones42903]

Some final thoughts on cycloidal clock teeth

[Sam StonesParticipant @samstones42903]

Apologies to those not-into-clocks.

As with previous threads, I based the geometry of this wheel/pinion layout upon BS 978: Part 2 see…

**LINK**

and

**LINK**

In the previous threads on pinion/wheel meshing and depthing, I took it that the ‘optimum’ condition of meshing would occur when the respective PCD’s touched. Using CAD, (for the time being my easiest option), I decided to ‘go deeper’. An actual depthing exercise may prove this wrong.

Without truncating the tips of the wheel teeth or deepening the pinion teeth (to weaken them even further), the limit to closing the gap (from optimum) was 0.445mm when the wheel teeth bottomed out.

Having ducked the many hours of a full run through the fifteen pinion steps as before, my adjusted starting point revealed that at 0.4mm (0.045mm short of bottom), the trailing edge of the next wheel tooth was contacting the pinion tooth next in line.

For reference, the yellow dots indicate where contact is made, and where jamming may occur.

As a slight deviation, members may question the reason for ignoring root radii. Seen on the left of my illustration, un-radiused pinion teeth are so much weaker. Not only are they thinner at the root but the sharp notches invite premature failure. Even the (seemingly token) radius of Swiss Standard NHS 56704 appears insufficient.

I welcome your answers.

Sam

Edit – There was no smiley face in my original

Edited By Sam Stones on 02/03/2020 23:57:27

2nd edit – attempted to remove smiley face!!!

Edited By Sam Stones on 03/03/2020 00:00:59

3rd edit – Smiley face removed.

Edited By Sam Stones on 03/03/2020 00:02:48

[Michael GilliganParticipant @michaelgilligan61133]

It may be of some relevance that, in the 1952 version of BS 978 Part 2, there was a choice of three different addendum profiles for driven pinions … Typically used thus:

A for 10 teeth and over

B for 8 and 9 teeth

C for 6 and 7 teeth

MichaelG.

[roy entwistleParticipant @royentwistle24699]

Theory is OK but the best way to get a good mesh is to use a depthing tool and feel for it

Roy

[Martin KyteParticipant @martinkyte99762]

I would be interested in your definition of 'ideal' meshing. As a 'practical' clockmaker relying on test depthing to establish wheel centres I have not payed much attention to theory. However, I am given to understand that arranging the meshing action to occur after the line of centres ensures that the contact point between the wheel and the pinion moves outwards from either centre of rotation to eliminate any wedging action.

I would be interested in comments.

regards Martin

[John HaineParticipant @johnhaine32865]

The significance of the "line of centres" argument has been questioned – see the references cited in other threads on this topic started by Sam.

Using a depthing tool is not very practical if the plates are being laid out using DRO or CNC, and especially if ball races are used for the arbor bearings.

[Martin KyteParticipant @martinkyte99762]

Posted by John Haine on 03/03/2020 09:28:58:

Using a depthing tool is not very practical if the plates are being laid out using DRO or CNC, and especially if ball races are used for the arbor bearings.

Not sure if I get that argument. Whether you scribe your centres using a depthing tool or measure and punch the readings into a CAD design or lay out using DRO's makes no odds. You are still transferring the results of a practical meshing of the wheel and pinion pair you are actually going to use rather than relying on having made each to the theoretical design.

regards Martin

[Michael GilliganParticipant @michaelgilligan61133]

Posted by roy entwistle on 03/03/2020 08:55:28:

Theory is OK but the best way to get a good mesh is to use a depthing tool and feel for it

Roy

.

I presume that we are all aware of that, Roy

Sam is, I believe, simply trying to explore the reasons why the right mesh feels right.

MichaelG.

[Sam StonesParticipant @samstones42903]

In a former life of suffering endless report writing to which I was never fully tuned, we were encouraged to create a title that more than adequately posed the issue.

With a prompt from earlier, (good onya Michael) here’s my effort …

In clock making, how does the sweet-spot equate to the theory of cycloidal gear-meshing?

Before I reply to the above responses while risking repetition and appearing smug, my experience of clock building is a one-off skeleton clock designed by Mr John Stevens. I drilled the pivot holes into the plates before I made the wheels and pinions. Although I eventually owned a copy of ‘Watch and clock making and repairing’, by Mr W J Gazeley it was already too late to apply the recommended method of depthing.

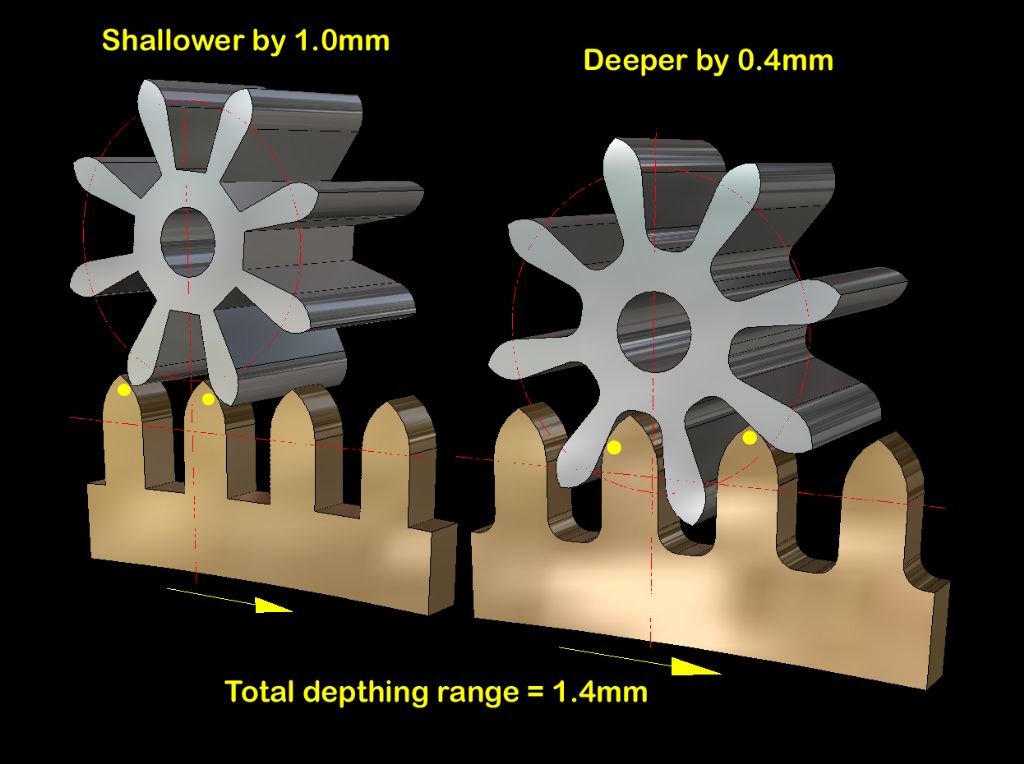
Well may you shudder at the ugly tooth shapes I generated. Here’s the evidence …

… but it worked and they are not even cycloidal or involute.

Well, the clock ticked unaided first time around.

John, Jumping ahead, I would have been in deep poo had I been fitting ball bearings, and the clock didn’t work.

Thanks Michael on at least two counts. I forgot to mention that I had returned to applying the theory to the 290-8 wheel/pinion pair in the Wilding large wheel design, while continuing blindly to follow the BS 978 data. This latter item along with the Swiss Standard NHS 56702, 3, and 4 was presumably, developed with a great deal of cerebral input with an eye on economy. The A, B, C of tooth addenda you highlighted just adds further to the complexity of surpassing practical depthing with a theoretical solution. Also, your observations put succinctly as always, address what I’m getting at.

Roy, I fully align with your comments, if only I had more than CAD.

Martin, At a theoretical level, cos that’s all I’ve got, I imagine ‘ideal meshing’ to be a sort of sweet spot where, subjectively, the transfer of energy is both smooth and efficient. How it’s achieved at a theoretical level, I can only imagine the requirement of a high degree of complexity.

Doesn’t the variable level of friction (from [tooth] entry to exit), further complicate a definitive solution?

This, to some extent, repeats the questions – Is there (likely to be) much of a detectable difference between the theoretical pivot centres as per the standards and those for the sweet spot, wherever the latter may be?

What allowance for tooth wear is necessary? I’m really out of my depth (pun?) here.

Finally, an apology is required in that I failed to notice that the Swiss standards actually show a full (semicircular) root radius.

Sam

[Martin KyteParticipant @martinkyte99762]

Again speaking from a pure practical approach, Clock gearing is by nature very different to 'normal' gearing. Primarily because wheels drive pinions but also because low friction becomes more desireable, than for example constant velocity ratios. Whilst acknowedging theory as a good starting point in developing a design serious consideration must also be given to the realities as they exist in the clock train.

All wheels and pinions have some degree of run out.

Pivots need to be free running so have a degree of 'slop' (If it rattles it will run is a well and appropriately used phrase regarding clocks)

Tooth form, spacing and wheel and pinion radii are never exact.

So whilst good theory gets you to the right ball park, select on test refines the result.

Thanks anyway for the interesting thread, I,m always more than happy to have my understanding modified and improved.

regards Martin

[roy entwistleParticipant @royentwistle24699]

Martin

Sam I don't have CAD, I don't even do drawings. I mark straight onto the plates. And over the years I have made over a dozen clocks

Roy

[Neil WyattModerator @neilwyatt]

Pah, Sam, it works which is what counts

Interesting that you seem to have rediscovered the tooth form used to make the Antikythera Mechanism.

Neil

[SillyOldDufferModerator @sillyoldduffer]

Posted by roy entwistle on 04/03/2020 09:33:30:

Martin

Sam I don't have CAD, I don't even do drawings. I mark straight onto the plates. And over the years I have made over a dozen clocks

Roy

The differences between amateur and industrial practice fascinate me.

Roy, I'm sure, makes beautiful clocks. Being packed full of craftsmanship and individuality makes a handmade mechanical clock a wonderful meld of art and science. Although the science part of timekeeping is brutally black and white there's plenty of room in Roy's work for personality.

The downside of Roy's approach leaps out when he says: 'over the years I have made over a dozen clocks'. Considered as an industrial process, Roy's methods are far too slow, requiring a skilled operator and lots of time. Not acceptable if the goal is to sell 10,000,000 movements for £10 each and make £2M profit.

High-accuracy techniques allow movements to be designed for production in the certainty they will work reliably for at least the guaranteed life of the clock. Parts are made precisely enough to assemble interchangeably without fitting, ideally not requiring trained production workers at all. Clocks made by this method require accurate well-maintained tooling and tight quality control rather than skill. Optimising the tooth form and mesh is an important part of the design because the intent is to minimise cost, partly by eliminating traditional clock-makers.

At the other extreme, I made two clocks in Meccano. One used a verge and spring-motor, the other a pendulum and weight. Meccano is too crude to make a good clock. Nonetheless, I was able to get both of them to work. Impressive novelties rather than reliable time-keepers, difficult to adjust and keep running. However, they proved clocks can be very rough indeed and still work. (Sort of!)

Like all engineering, clocks are about using the technique that best meets the requirement. What I did with Meccano is useless to a proper clockmaker like Roy, and what Roy does is useless to an industry that's moved largely to mass producing very simple plastic movements driven by accurate electronic oscillators. In most ordinary modern clocks any beauty is in the casing, not the innards. I find them soulless compared with home-made mechanical clocks which are full of character and interest – even when the home-made clocks don't work!

I find Sam's investigations interesting and get to benefit from Roy's practical view. Excellent – I find both points of view useful.

Dave

Edited By SillyOldDuffer on 04/03/2020 10:49:26

[roy entwistleParticipant @royentwistle24699]

Dave

Thank you

Roy

[Martin KyteParticipant @martinkyte99762]

The differences between amateur and industrial practice fascinate me.

Parts are made precisely enough to assemble interchangeably without fitting, ideally not requiring trained production workers at all. Clocks made by this method require accurate well-maintained tooling and tight quality control rather than skill.

Or sometime designs are as they are so that the largest tolerances are acceptable and you still get a working clock.

regards Martin

[John HaineParticipant @johnhaine32865]

For me the interest in Sam's work is in understanding what compromises (if any) result from the fact the real clock tooth forms are not epicycloidal (except for straight radial pinion flanks) but approximations using circles. I wonder how much analysis actually went into the British and Swiss standards – or (as in much standards work) did they just find a mutually agreeable compromise?

Regarding experimental rather than theoretical depthing, I know of at least one clockmaker who lays out the plates of beautifully made and running clocks using CNC, and therefore needs to know the optimum depth in advance. Given the required tolerance, it is hard to do this by making measurements on the depthing tool. Also, what is the "feel" criterion for good engagement? If the gear axes are too far apart, so the pinion addendum starts to get involved, it will certainly feel rather "notchy". Too small and fouling might start either with the following teeth or the pinion roots. What's the characteristic of the sweet spot in between, how critical is it, and how much will different makers differ in their judgement? And given that the torque applied to the gears in the depthing tool will almost certainly be much less than they will carry in service at least near the spring or weight barrel, is the "feel" depth best for every gear pair in the train?

Finally, now we can generate gears directly from software via CNC (using e.g. Gearotic), could better gears be designed than just by using the standards?

[Martin KyteParticipant @martinkyte99762]

Posted by John Haine on 04/03/2020 13:07:28:

For me the interest in Sam's work is in understanding what compromises (if any) result from the fact the real clock tooth forms are not epicycloidal (except for straight radial pinion flanks) but approximations using circles. I wonder how much analysis actually went into the British and Swiss standards – or (as in much standards work) did they just find a mutually agreeable compromise?

Regarding experimental rather than theoretical depthing, I know of at least one clockmaker who lays out the plates of beautifully made and running clocks using CNC, and therefore needs to know the optimum depth in advance. Given the required tolerance, it is hard to do this by making measurements on the depthing tool.

 

It's not beyond the wit of man to come up with a depthing tool with it's own DRO surely. However I agree that 'feel' is somewhat subjective.

I do remember a lecture given by Alec Price some years ago who laid very little weight on correct tooth forms. In fact if you look at many/most ancient clocks by the famous or not so famous makers of days gone by you will find many strange looking tooth forms. One of the overriding factors in tooth form is how easy is it to make the cutters.

Single point cutters of approximate shape are easy to make when you only have to generate straight lines and arcs of a circle.

 

regards Martin

Edited By Martin Kyte on 04/03/2020 13:36:48

Edited By Martin Kyte on 04/03/2020 13:37:11

[Michael GilliganParticipant @michaelgilligan61133]

Posted by John Haine on 04/03/2020 13:07:28:

For me the interest in Sam's work is in understanding what compromises (if any) result from the fact the real clock tooth forms are not epicycloidal (except for straight radial pinion flanks) but approximations using circles. I wonder how much analysis actually went into the British and Swiss standards – or (as in much standards work) did they just find a mutually agreeable compromise?

Regarding experimental rather than theoretical depthing, I know of at least one clockmaker who lays out the plates of beautifully made and running clocks using CNC, and therefore needs to know the optimum depth in advance. Given the required tolerance, it is hard to do this by making measurements on the depthing tool. Also, what is the "feel" criterion for good engagement? If the gear axes are too far apart, so the pinion addendum starts to get involved, it will certainly feel rather "notchy". Too small and fouling might start either with the following teeth or the pinion roots. What's the characteristic of the sweet spot in between, how critical is it, and how much will different makers differ in their judgement? And given that the torque applied to the gears in the depthing tool will almost certainly be much less than they will carry in service at least near the spring or weight barrel, is the "feel" depth best for every gear pair in the train?

Finally, now we can generate gears directly from software via CNC (using e.g. Gearotic), could better gears be designed than just by using the standards?

.

John,

I think the first point of note might be that, for ‘predetermined’ centres, the involute tooth form is more forgiving of depthing errors than the cycloidal.

Second … regarding the Swiss and British standards: There is considerable detail, and [one might reasonably assume] some significant science underlying them. … ‘though how much of that is relevant to the amateur maker or repairer remains questionable.

MichaelG.

.

P.S. it’s good to see that TEE has republished Owen’s book

https://www.teepublishing.co.uk/books/gears/gears-for-small-mechanisms/

Edited By Michael Gilligan on 04/03/2020 14:02:19

[John HaineParticipant @johnhaine32865]

Posted by Michael Gilligan on 04/03/2020 13:56:12:

Posted by John Haine on 04/03/2020 13:07:28:

John,

I think the first point of note might be that, for ‘predetermined’ centres, the involute tooth form is more forgiving of depthing errors than the cycloidal.

Second … regarding the Swiss and British standards: There is considerable detail, and [one might reasonably assume] some significant science underlying them. … ‘though how much of that is relevant to the amateur maker or repairer remains questionable.

MichaelG.

.

P.S. it’s good to see that TEE has republished Owen’s book

**LINK**

Edited By Michael Gilligan on 04/03/2020 14:02:19

Yes, the involute is more forgiving – but doesn't meet the "action after line of centres" criterion. As for the science, in areas of engineering that I am familiar with the ,behind design decisions is well known, but this doesn't seem to be the case for horological gear standards.

[John HaineParticipant @johnhaine32865]

Posted by John Haine on 04/03/2020 15:50:19:

Posted by Michael Gilligan on 04/03/2020 13:56:12:

Posted by John Haine on 04/03/2020 13:07:28:

John,

I think the first point of note might be that, for ‘predetermined’ centres, the involute tooth form is more forgiving of depthing errors than the cycloidal.

Second … regarding the Swiss and British standards: There is considerable detail, and [one might reasonably assume] some significant science underlying them. … ‘though how much of that is relevant to the amateur maker or repairer remains questionable.

MichaelG.

.

P.S. it’s good to see that TEE has republished Owen’s book

**LINK**

Edited By Michael Gilligan on 04/03/2020 14:02:19

Yes, the involute is more forgiving – but doesn't meet the "action after line of centres" criterion. As for the science, in areas of engineering that I am familiar with the ,behind design decisions is well known, but this doesn't seem to be the case for horological gear standards.

Um, Davis' book?

[duncan webster 1Participant @duncanwebster1]

Apologies if this has been linked before, but it seems to debunk cycloidal gears completely

**LINK**

to quote the opening paragraph…….'The cycloidal tooth would never be missed if it were dropped altogether….

[Martin KyteParticipant @martinkyte99762]

Posted by duncan webster on 04/03/2020 16:13:02:

Apologies if this has been linked before, but it seems to debunk cycloidal gears completely

**LINK**

to quote the opening paragraph…….'The cycloidal tooth would never be missed if it were dropped altogether….

First it is important to acknowledge that the coefficient of friction for approach action cannot be different from that for recess action, for when Leonardo da Vinci slid weights across a table, observing that "Friction produces double the amount of effort if the weight be doubled," he didn't have to differentiate between pushing (approach) and pulling (recess)

That is true for free moving sliding weights. However if the resultant of the frictive vector and the normal force vector acting on a pinion is such direction as to pass behind the centre of rotation it will act to increase the normal force vector which increases the frictive force vector in consequence hence the wedging action.

Personally I would always use cycloidal on small clocks if only for the look of the wheels. Tower clock are different animals and for them involute wins hands down if only because you get a stronger tooth.

regards Martin

[Michael GilliganParticipant @michaelgilligan61133]

Posted by John Haine on 04/03/2020 15:51:15:

Um, Davis' book?

.

Oops

… well, at least it saved me worrying about whether to write Davis’ or Davis’s

• Wilfred Owen Davis, Engineer, Research Department, Aviation Division, S. Smith & Sons (England) Ltd.

MichaelG.

[Sam StonesParticipant @samstones42903]

With no intentions of appearing gender biased, I was brought to my senses by what appears to be a sign of the times when MS Word underlined in blue my use of the word ‘gentlemen’.

So I tried gentle men, and guess what, MS Word responded with the instruction to use ‘gentlemen’!

And all I wanted to say was ‘Gentlemen, Thank you for your interest and contributions!’

Sam

Any tin hats to spare?

[Sam StonesParticipant @samstones42903]

Neil wrote … Pah, Sam, it works which is what counts

Thanks Neil, and well spotted.

Had I been more observant before cutting my own clock teeth, I could have taken the easier route of a radiused cycloidal addenda. Instead, mine were a botched up involute, a recollection from night school perhaps.

I’m sure too, you know better than I that, as with ordinary wheels (which were originally square until the corners wore off), most of the Antikythera gear teeth appear to be triangular and nothing like cycloidal. At least that’s how Chris of Clickspring has cut his Antikythera teeth.

**LINK**

Martin, Thanks for the prompting re force vectors. I couldn’t think of how to apply the potential variance between entry and exit friction. Maybe I’ll fire up the laptop and ponder some more.

Sam

[Author]

Posts