Myford ml7 21 tooth change gears

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Rufus Roughcut on 03/01/2016 16:34:57:

… has anyone tried jacking up a Myford 7

.

Rufus,

as I mentioned earlier; Martin Cleeve had a tidier solution:

MichaelG.

Martin Cleeve's use of a reduced pitch 127 tooth, mixed in the Myford train, is maybe my source of 'inspiration'.

[Rufus RoughcutParticipant @rufusroughcut]

Hi Michael

I see the different pitches and DPs of gears can be mixed without direct meshing throughout a train by use of the stubs, out of sad interest I have a T104 like the one on the lead screw which meshes fine with the myford gears but have absolutely no idea what use it may be, along with a small box of similar rogue number tooth gears, it's also worth saying I do check mine against the myfords and my hobs before running them together I'm not quite that rough yet.

Great concept though, I'm getting tempted to get my spare ML10 out and play

Rufus

[TendorParticipant @tendor]

John Stevenson’s comment about 60/63 being used “instead of” 120/127 might, for some, leave the impression that the approximation comes about because 63 is the closest integer to one half of 127 and is, in comparison, compact and hence more convenient. But not so – the error would be one part in 126 (or 127 for their reciprocals). As stated in other posts, a 127 tooth gear will produce a mathematically exact metric pitch on an imperial lead screw, being the exact number of mm in 5 inches and the lowest integer pair that expresses this exact relationship.

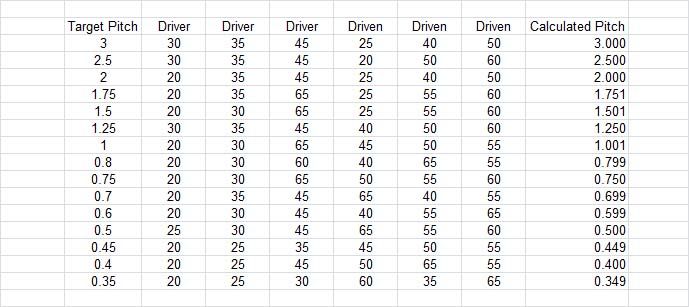
For metric pitches using an 8 tpi leadscrew, the exact desired conversion ratio is 25.4/8 mm per one leadscrew pitch, or 25.4/8 = 127/40 = (127/100) x 2.5 = 3.175 (exactly). It just happens that this is closely approximated by 200/63 = (80/63) x 2.5 = 3.174603…, just 1 in 8001 smaller (12.5 microns per 100 mm, or 0.0005” per 4".

Notice though, that whereas the 127 tooth gear forms the numerator (a driven gear), the 63 tooth gear forms the denominator (a driver gear). It is not performing the duty of an approximate 127 tooth driven gear (i.e. not 63 x 2 approx. equals 127). The actual comparison is between the ratios 127/100 and 80/63 (ignoring the 2.5 common multiplier).

Since 21 and 3 are factors of 63, a 21 tooth gear can also serve as a driver, with the factor of 3 formed by other train gears. For example, a 1 mm pitch from an 8 tpi lead screw requires a lead screw to spindle turns ratio of 63/200 = for example (21/40)·(30/50),  or, as per Roderick's table, (45/40).(21/75)

Edited By Rodney Entwistle on 14/01/2016 06:36:48

Edited By Rodney Entwistle on 14/01/2016 06:37:28

Edited By Rodney Entwistle on 14/01/2016 06:58:45

Edited By Rodney Entwistle on 14/01/2016 07:00:14

[Michael GilliganParticipant @michaelgilligan61133]

Good summary, Rodney

MichaelG.

[Roderick JenkinsParticipant @roderickjenkins93242]

That's the first really clear explanation I've seen of why a 63 (or 21) tooth gear works so well, as a driver, for metric conversion.

Many thanks,

Rod

[Neil WyattModerator @neilwyatt]

Posted by Roderick Jenkins on 14/01/2016 09:26:10:

That's the first really clear explanation I've seen of why a 63 (or 21) tooth gear works so well, as a driver, for metric conversion.

Shame on you Rod, you must have missed the excellent article in MEW 204

Neil

[Roderick JenkinsParticipant @roderickjenkins93242]

Posted by Neil Wyatt on 14/01/2016 09:47:56:

Shame on you Rod, you must have missed the excellent article in MEW 204

I did. As it concerned a mini lathe I merely skimmed it – that will teach me not to be parochial

Rod

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Roderick Jenkins on 14/01/2016 10:05:58:

Posted by Neil Wyatt on 14/01/2016 09:47:56:

Shame on you Rod, you must have missed the excellent article in MEW 204

I did. As it concerned a mini lathe I merely skimmed it –

.

… and therein lies the importance of indexing, cross-referencing,

'allocation to forum topic', and all that tedious stuff.

.

MichaelG.

Edited By Michael Gilligan on 14/01/2016 10:33:18

[Neil WyattModerator @neilwyatt]

Posted by Michael Gilligan on 14/01/2016 10:31:30:

… and therein lies the importance of indexing, cross-referencing,

'allocation to forum topic', and all that tedious stuff.

I thought you would be the champion of search engines which allow us to abandon all that 20th-century stuff

Neil

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Neil Wyatt on 15/01/2016 10:45:25:

I thought you would be the champion of search engines which allow us to abandon all that 20th-century stuff

.

That, Neil, is the whole point … There is no search engine that can reliably find things that have inadequate references.

MichaelG.

[Neil WyattModerator @neilwyatt]

Posted by Michael Gilligan on 15/01/2016 10:59:46:

Posted by Neil Wyatt on 15/01/2016 10:45:25:

I thought you would be the champion of search engines which allow us to abandon all that 20th-century stuff

.

That, Neil, is the whole point … There is no search engine that can reliably find things that have inadequate references.

MichaelG.

I won't keep this going beyond one response, as we are wandering OT, but I think the joy of search engines is that when references are inadequate they provide just about the only way of finding things.

Several years ago the vaguely remembered phrase 'The queech obulates' returned no hits… it now gives many relevant results and last year allowed me to finally tack down the source.

I was also able to find the origin of the 'Green Meat Saga' from my childhood – in an RAF yearbook.

They may not do so reliably but I am convinced they do so better than any other way.

Neil

[Michael GilliganParticipant @michaelgilligan61133]

Back on topic:

There are many 'calculators' available, both on-line and off-line, but I rather like this one for its versatility: **LINK**

MichaelG.

[BWParticipant @bw]

Michael,

Thankyou for that link – its brilliant.

Allows user to input a target thread of 25.4 tpi whilst using a 8tpi leadscrew. and will then calculate closest gear combinations.

Bill

[BWParticipant @bw]

Did some looking around. ……. That web page gear calculator has been converted to an apk file that can be downloaded from here

http://mynewlathe.blogspot.co.uk/ – see post approx 1/4 way down the page.

My only problem is I dont know what to do with an apk file – do I simply copy it to my tablet or do I have to execute it somehow ?

And I think this link is relevant, useful and on topic if you want to generate templates to divide 21, 33, 34, 63 etc

http://www.cgtk.co.uk/metalwork/reference/divider

Bill

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Bill Wood 2 on 16/01/2016 06:44:46:

And I think this link is relevant, useful and on topic if you want to generate templates to divide 21, 33, 34, 63 etc

http://www.cgtk.co.uk/metalwork/reference/divider

.

Bill,

I'm glad to see you found CGTK's 'Divider Wheel Generator'

I have posted that **LINK** several times on this forum, but [ref. my recent 'off-topic' discussion with Neil] people still seem to have difficulty finding it when they need it.

MichaelG.

[Michael GilliganParticipant @michaelgilligan61133]

Posted by Bill Wood 2 on 16/01/2016 06:44:46:

My only problem is I dont know what to do with an apk file – do I simply copy it to my tablet or do I have to execute it somehow ?

.

Bill,

I haven't checked them yet, but these instructions look good.

MichaelG.

[BWParticipant @bw]

Many thanks for the info on this thread ……..

So ……….. I can "cheat" occassionally and use these dinky little timing pulleys and a toothed belt instead of meshing gears together ……….. I imagine it would be easier to make these "flat" teeth than to make the cutter I've ground to match the profile of my current gears.

I was going to cut a pair of gears 47/37 = 1.27027027 and introduce that into my gear train but after reading this thread I think I can do

21 drives 40-30 drives 56 then gearbox

I think I can cut a 21 and a 30 and then use my gearbox ratios to produce metric threads …. and thats a lot less teeth to cut.

Will go and do some more playing with spreadsheets to check it out, have got a Hercus 9" lathe with a gearbox, Hercus is Australian equivalent of South Bend. Gearbox ratios probably different to Myford but the maths and ratios should still allow me a way through …………

Heres a picture of my lathe http://metalworkforums.com/attachment.php?attachmentid=308680&d=1395972160

Bill

[Roderick JenkinsParticipant @roderickjenkins93242]

I have enormous admiration for the people who calculated metric approximations by analytical means using translation gears but since it's it's a cold, damp, indoor afternoon here in Hampshire, I thought I'd have a go with the scattergun approach using my Excel/visual Basic calculator. Many older British lathes had a fairly basic changewheel set of 20-65 in steps of 5 and an 8tpi leadscrew (such as my old Zyto). Using only these I get the following table for all the usual metric coarse and fine threads that you might want to screwcut::

I'm not saying that you can get every combination to mesh on the banjo but I think it is quite interesting that no thread is more than a micron out! This is better than I got with a PET2000 some decades ago but I think that's because the calculations take a second, not overnight, and I'm letting them carry on to a smaller error.

Rod

[Michael GilliganParticipant @michaelgilligan61133]

Nicely done, Rod

Some very good results from a small collection of change-wheels.

MichaelG.

[Roderick JenkinsParticipant @roderickjenkins93242]

I think it's just an example that somewhere within all the combinations of changewheels is the required set for most threads to a practical accuracy. Even on the fairly small set mentioned above there are (I think) 4,200* unique combinations.

* 10C3 x 7C3 – is that correct?

Rod

Edited By Roderick Jenkins on 17/01/2016 16:15:28

[BWParticipant @bw]

Posted by Neil Wyatt on 14/01/2016 09:47:56:

Posted by Roderick Jenkins on 14/01/2016 09:26:10:

That's the first really clear explanation I've seen of why a 63 (or 21) tooth gear works so well, as a driver, for metric conversion.

Shame on you Rod, you must have missed the excellent article in MEW 204

Neil

From Issue 204 : These should be cut by thread milling, using the leadscrew to turn the mandrel with the lathe switched off. To dothis a toolpost milling spindle and a leadscrew handwheel such as that described by Alastair Sinclair (Model Engineer’s Workshop, issue 91, July 2003) will be needed.

Am curious ……… what would the milling cutter look like in the thread milling process described above ? Would it be a very skinny vee shaped end mill ? or a chunky slitting saw with a vee shaped cutting profile ?

[Neil WyattModerator @neilwyatt]

Posted by Bill Wood 2 on 14/09/2016 14:16:14:

Posted by Neil Wyatt on 14/01/2016 09:47:56:

Posted by Roderick Jenkins on 14/01/2016 09:26:10:

That's the first really clear explanation I've seen of why a 63 (or 21) tooth gear works so well, as a driver, for metric conversion.

Shame on you Rod, you must have missed the excellent article in MEW 204

Neil

From Issue 204 : These should be cut by thread milling, using the leadscrew to turn the mandrel with the lathe switched off. To dothis a toolpost milling spindle and a leadscrew handwheel such as that described by Alastair Sinclair (Model Engineer’s Workshop, issue 91, July 2003) will be needed.

Am curious ……… what would the milling cutter look like in the thread milling process described above ? Would it be a very skinny vee shaped end mill ? or a chunky slitting saw with a vee shaped cutting profile ?

From memory, you are referring to my comment on making threads with a pitch significantly greater than the leadscrew.

The usual cutter shape is like a gear cutter, (sort of like a chunky slitting saw but with about 10 or 12 teeth) obviously shaped to match the thread profile.

You can make and use a single point cutter but it's a lit slower.

In principle a shaped end mill would work, but you are talking a lot of effort to make one unless you need a square thread.

Neil

[BWParticipant @bw]

Posted by Michael Gilligan on 29/12/2015 17:52:04:

This 21 tooth Timing Pulley may be of interest.

I bought 'the last one' today, but presumably there will more available sometime.

MichaelG.

I've been pondering this 21 tooth pulley and the following photo posted by John S.

I found this link for different belt lengths – https://sdp-si.com/eStore/..%5Css%5CPDF%5C15501003.pdf – and I note one can buy the belt by the metre and make your own custom belt lengths, cannot find many different sized big wheels (found a few up to 36 teeth nothing bigger) to stick at the other end of the belt from the 21 tooth – have concluded that it would be a pain to make them. What should I search for please ? Are these standard items I would know more about if I was conversant with cnc machines and 3d printers ?

Bill

[BWParticipant @bw]

OK,

Please ignore previous post.

Found a heap of 1/5" timing wheels up to 72 teeth here http://www.globalindustrial.com/g/motors/timing-belts/aluminum-timing-belt-pulleys/XL-1-5-pitch

So as per Michael G's post can see how to run a hybrid sysem with a 21 drives XX joined onto a standard change wheel.

Thankyou Michael – good idea – have bought a 21 tooth for $5.47

Bill

[Jon CameronParticipant @joncameron26580]

Hi, I'm sorry for resurrecting an old 'thread', but would any of the combinations of gears be useable with a myford ML4 I have been told the lead screws are the same pitches, if not identical. Which would only leave the small gear wheel on the spindle as a variable? My lathe is pretty much still all imperial. Even after all these years.

[Author]

Posts