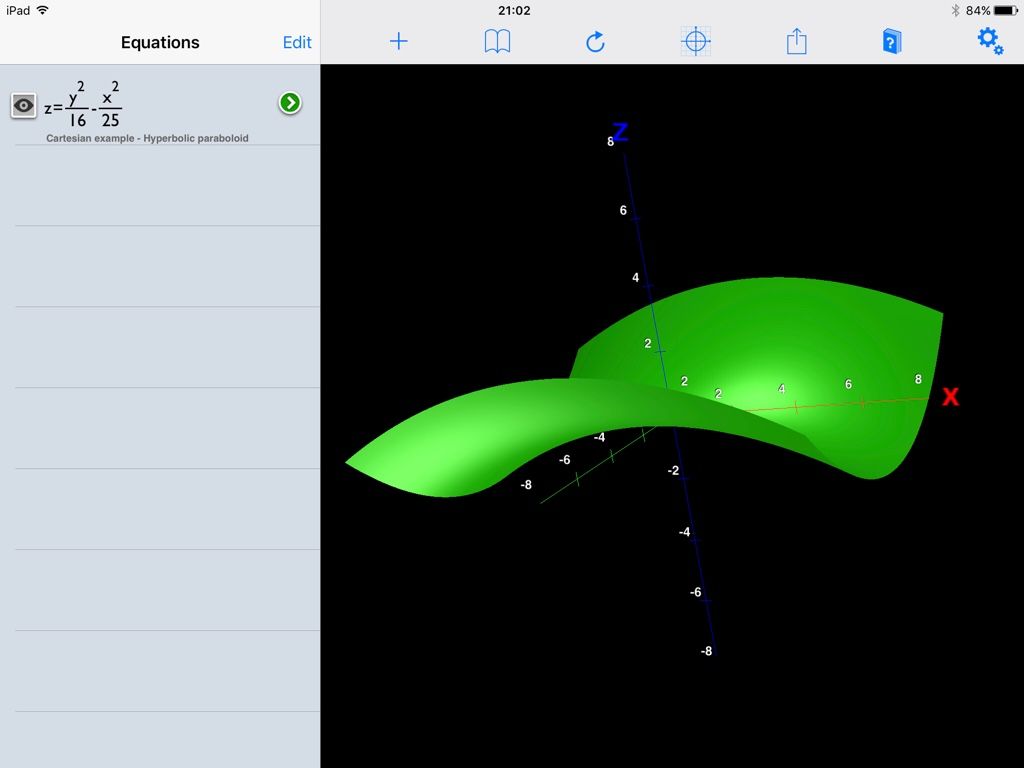
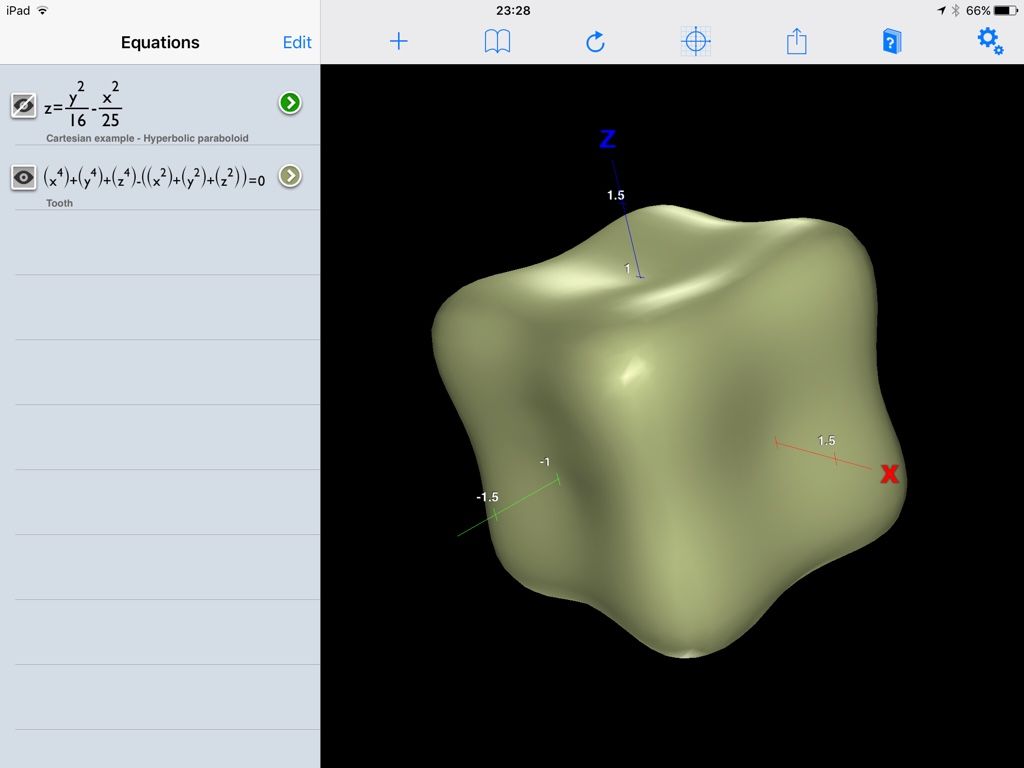
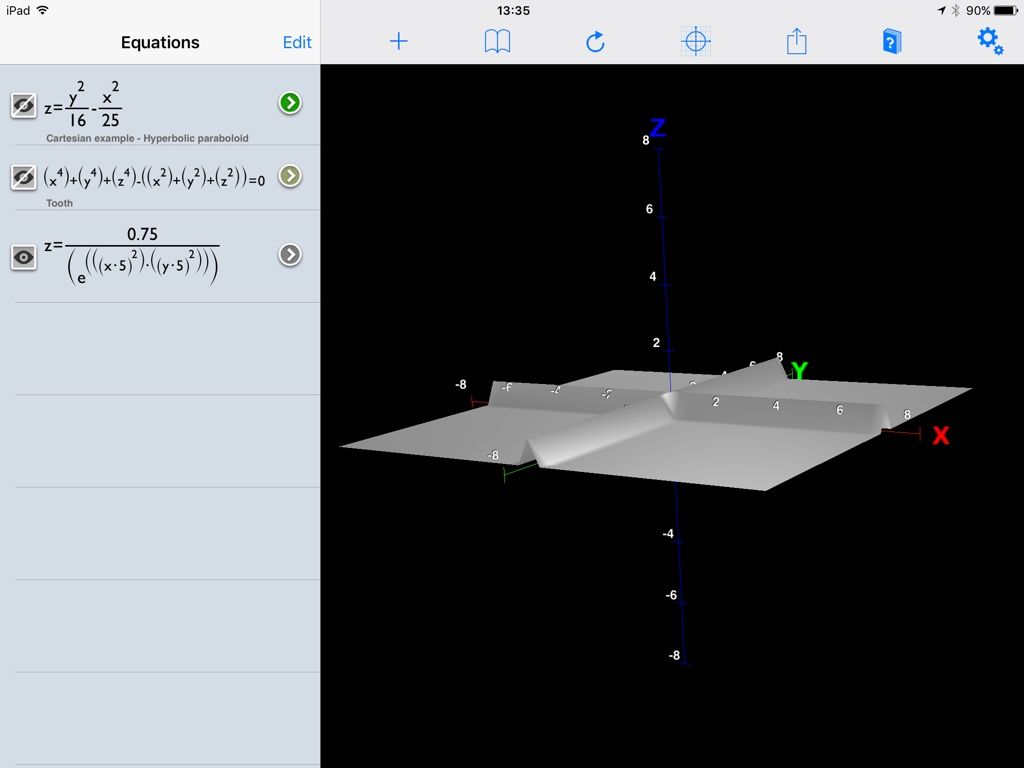
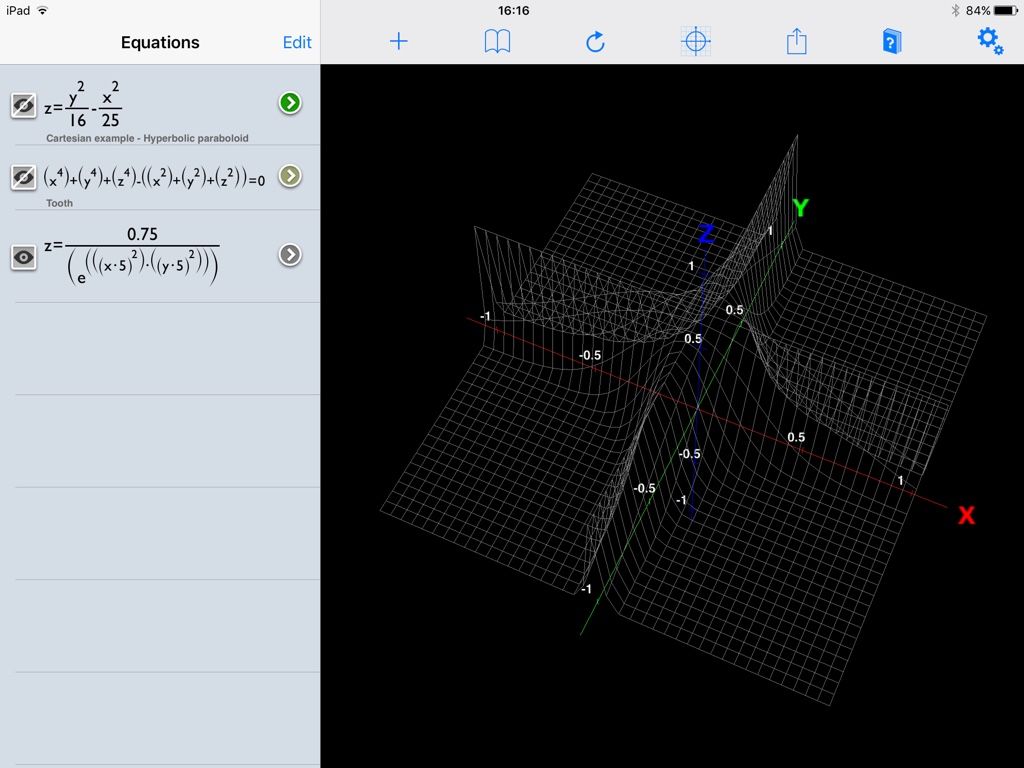
3D graphing of mathematical functions
3D graphing of mathematical functions
- This topic has 57 replies, 16 voices, and was last updated 27 December 2016 at 15:10 by
 Michael Gilligan.
Michael Gilligan.
- Please log in to reply to this topic. Registering is free and easy using the links on the menu at the top of this page.
Latest Replies
Viewing 25 topics - 1 through 25 (of 25 total)
-
- Topic
- Voices
- Last Post
Viewing 25 topics - 1 through 25 (of 25 total)
Latest Issue
Newsletter Sign-up
Latest Replies
- design and use of cutting tools
- Vallder CNC
- What Did You Do Today 2025
- Denford Orac refit
- Safe and secure way to suspend a 5″G Tender
- Alternatives for a DRO display change
- Swing over bed limitation for flywheels
- Big Vise, go big or go home
- Parting off on a mini lathe
- St Albans Big Show 27 & 28 Sept 25