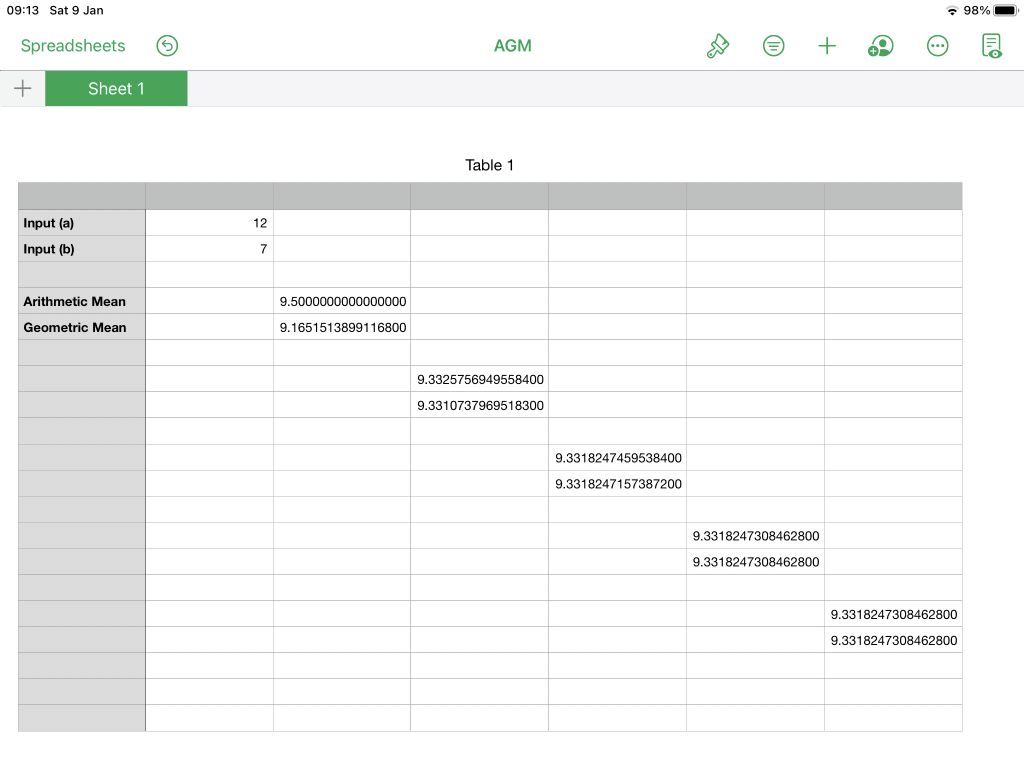
A not-so-new Pendulum formula
A not-so-new Pendulum formula
- This topic has 8 replies, 5 voices, and was last updated 9 January 2021 at 10:44 by
 Michael Gilligan.
Michael Gilligan.
Viewing 9 posts - 1 through 9 (of 9 total)
Viewing 9 posts - 1 through 9 (of 9 total)
- Please log in to reply to this topic. Registering is free and easy using the links on the menu at the top of this page.
Latest Replies
Viewing 25 topics - 1 through 25 (of 25 total)
-
- Topic
- Voices
- Last Post
Viewing 25 topics - 1 through 25 (of 25 total)
Latest Issue
Newsletter Sign-up
Latest Replies
- 3 phase supply (again)
- Arc Euro Trade Ltd.
- My week this week! My workshop videos
- Steam driven air pump for brakes
- Herbert B Drill Pulley and Lubrication
- MicroSet3 timer – help to set for tacho
- Raab Style Heibluftmotor
- New member – mid 50s Zyto Lathe
- Making Unimat DB/SL Steadies
- Reference lines for dimensions – Fusion 360